Performs a k-sample trends test against ordered alternatives.
Synopsis
#include <imsls.h>
float *imsls_f_ k_trends_test (int n_groups, int ni[], float y[], ..., 0)
The type double function is imsls_d_ k_trends_test.
Required Arguments
int n_groups
(Input)
Number of groups. Must be greater than or equal to
3.
int ni[]
(Input)
Array of length n_groups containing
the number of responses for each of the n_groups
groups.
float y[]
(Input)
Array of length ni[0] + ... +
ni[n_groups-1] that contains the responses for each of the n_groups
groups. y must
be sorted by group, with the ni[0] observations in
group 1 coming first, the ni[1] observations in
group two coming second, and so on.
Return Value
Array of length 17 containing the test results.
I stat[I]
0 Test statistic (ties are randomized).
1 Conservative test statistic with ties counted in favor of the null hypothesis.
2 p-value associated with stat[0].
3 p-value associated with stat[1].
4 Continuity corrected stat[2].
5 Continuity corrected stat [3].
6 Expected mean of the statistic.
7 Expected kurtosis of the statistic. (The expected skewness is zero.)
8 Total sample size.
9 Coefficient of rank correlation based upon stat[0].
10 Coefficient of rank correlation based upon stat[1].
11 Total number of ties between samples.
12 The t-statistic associated with stat [2].
13 The t-statistic associated with stat[3].
14 The t-statistic associated with stat [4].
15 The t-statistic associated with stat[5].
16 Degrees of freedom for each t-statistic.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_k_trends_test (int
n_groups, int
ni, float
y[],
IMSLS_RETURN_USER,
float
stat[], 0)
Optional Arguments
IMSLS_RETURN_USER, float stat[]
(Output)
User defined array for storage of test results.
Description
Function imsls_f_k_trends_test performs a k-sample trends test against ordered alternatives. The alternative to the null hypothesis of equality is that F1(X) < F2(X) < … Fk(X), where F1, F2, etc., are cumulative distribution functions, and the operator < implies that the less than relationship holds for all values of X. While the trends test used in k_trends_test requires that the background populations be continuous, ties occurring within a sample have no effect on the test statistic or associated probabilities. Ties between samples are important, however. Two methods for handling ties between samples are used. These are:
1. Ties are randomly split (stat[0]).
2. Ties are counted in a manner that is unfavorable to the alternative hypothesis (stat[1]).
Computational Procedure
Consider the matrices
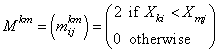
where Xki is the i-th observation in the k-th population, Xmj is the j-th observation in the m-th population, and each matrix Mkm is nk by nm where ni = ni(i). Let Skm denote the sum of all elements in Mkm. Then, stat[1] is computed as the sum over all elements in Skm, minus the expected value of this sum (computed as
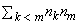
when there are no ties and the distributions in all populations are equal). In stat[0], ties are broken randomly, and the element in the summation is taken as 2.0 or 0.0 depending upon the result of breaking the tie.
stat[2]
and stat[3]
are computed using the t distribution. The probabilities reported are
asymptotic approximations based upon the t statistics in stat[12]
and stat[13],
which are computed as in Jonckheere (1954, page 141).
Similarly, stat[4]
and stat[5]
give the probabilities for stat[14]
and stat[15],
the continuity corrected versions of stat[2]
and stat[3].
The degrees of freedom for each t statistic (stat[16])
are computed so as to make the t distribution selected as close as
possible to the actual distribution of the statistic (see Jonckheere 1954, page
141).
stat[6], the variance of the test statistic stat[0], and stat[7], the kurtosis of the test statistic, are computed as in Jonckheere (1954, page 138). The coefficients of rank correlation in stat[8] and stat[9] reduce to the Kendall τ statistic when there are just two groups.
Exact probabilities in small samples can be obtained from tables in Jonckheere (1954). Note, however, that the t approximation appears to be a good one.
Assumptions
1. The Xmi for each sample are independently and identically distributed according to a single continuous distribution.
2. The samples are independent.
Hypothesis tests
H0 : F1(X)
≥ F2(X)
≥ … ≥ Fk(X)
H1 : F1(X)
< F2(X)
< … < Fk(X)
Reject if stat[2]
(or stat[3],
or stat[4]
or stat[5],
depending upon the method used) is too large.
Example
The following example is taken from Jonckheere (1954, page 135). It involves four observations in four independent samples.
#include <imsls.h>
#include <stdio.h>
int main()
{
float *stat;
int n_groups = 4;
int ni[] = {4, 4, 4, 4};
char *fmt = "%9.5f";
char *rlabel[] = {
"stat[0] - Test Statistic (random) .............",
"stat[1] - Test Statistic (null hypothesis) ....",
"stat[2] - p-value for stat[0] .................",
"stat[3] - p-value for stat[1] .................",
"stat[4] - Continuity corrected for stat[2] ....",
"stat[5] - Continuity corrected for stat[3] ....",
"stat[6] - Expected mean .......................",
"stat[7] - Expected kurtosis ...................",
"stat[8] - Total sample size ...................",
"stat[9] - Rank corr. coef. based on stat[0] ...",
"stat[10]- Rank corr. coef. based on stat[1] ...",
"stat[11]- Total number of ties ................",
"stat[12]- t-statistic associated w/stat[2] ....",
"stat[13]- t-statistic asscoiated w/stat[3] ....",
"stat[14]- t-statistic associated w/stat[4] ....",
"stat[15]- t-statistic asscoiated w/stat[5] ....",
"stat[16]- Degrees of freedom .................."};
float y[] = {19., 20., 60., 130., 21., 61., 80., 129.,
40., 99., 100., 149., 49., 110., 151., 160.};
stat = imsls_f_k_trends_test(n_groups, ni, y, 0);
imsls_f_write_matrix("stat", 17, 1, stat,
IMSLS_WRITE_FORMAT, fmt,
IMSLS_ROW_LABELS, rlabel,
0);
}
Output
stat(0) - Test statistic (random) ........... 46.00000
stat(1) - Test statistic (null hypothesis) .. 46.00000
stat(2) - p-value for stat(0) ............... 0.01483
stat(3) - p-value for stat(1) ............... 0.01483
stat(4) - Continuity corrected stat(2) ...... 0.01683
stat(5) - Continuity corrected stat(3) ...... 0.01683
stat(6) - Expected mean ..................... 458.66666
stat(7) - Expected kurtosis ................. -0.15365
stat(8) - Total sample size ................. 16.00000
stat(9)- Rank corr. coef. based on stat(0) . 0.47917
stat(10)- Rank corr. coef. based on stat(1) . 0.47917
stat(11)- Total number of ties .............. 0.00000
stat(12)- t-statistic associated w/stat(2) .. 2.26435
stat(13)- t-statistic associated w/stat(3) .. 2.26435
stat(14)- t-statistic associated w/stat(4) .. 2.20838
stat(15)- t-statistic associated w/stat(5) .. 2.20838
stat(16)- Degrees of freedom ................ 36.04963
