Calculates forecasts for trained multilayered feedforward neural network.

Synopsis

#include <imsls.h>

float *imsls_f_mlff_network_forecast (Imsls_f_NN_Network *network, 
int n_nominal,  int n_continuous, 
int nominal[],  float continuous[], ..., 0)

The type double function is imsls_d_mlff_network_forecast.

Required Arguments

Imsls_f_NN_Network *network   (Input)
Pointer to a structure of type Imsls_f_NN_Network containing the trained feedforward network.  See imsls_f_mlff_network.

int n_nominal   (Input)
Number of nominal attributes.

int n_continuous   (Input)
Number of continous attributes. 

int nominal[]   (Input)
Array of size n_nominal containing the nominal input variables. 

float continuous[]   (Input)
Array of size n_continuous containing the continuous input variables.

Return Value

Pointer to an array of size n_outputs containing the forecasts, where n_outputs is the number of output perceptrons in the network. n_outputs = network->n_outputs.  This space can be released by using the imsls_free function.

Synopsis with Optional Arguments

#include <imsls.h>

float *imsls_f_mlff_network_forecast (Imsls_f_NN_Network *network,
int n_nominal,  int n_continuous,  int nominal[],
float continuous[],
IMSLS_RETURN_USER, float forecasts[], 
0)

Optional Arguments

IMSLS_RETURN_USER, float  forecasts[]  (Output)
If specified, the forecasts for the trained network is stored in a user-supplied array forecasts of size n_outputs, where n_outputs is the number of perceptrons in the network, n_outputs = network->n_outputs.

Description

Function imsls_f_mlff_network_forecast calculates a forecast for a previously trained multilayered feedforward neural network using the same network structure and scaling applied during the training.   The structure Imsls_f_NN_Network describes the network structure used to originally train the network. The weights, which are the key output from training, are used as input to this routine.  The weights are stored in the Imsls_f_NN_Network structure.

In addition, two one-dimensional arrays are used to describe the values of the nominal and continuous attributes that are to be used as network inputs for calculating the forecast.

Training Data

Neural network training data consists of the following three types of data:

1.             nominal input attribute data

2.             continuous input attribute data

3.             continuous output data

The first data type contains the encoding of any nominal input attributes.  If binary encoding is used, this encoding consists of creating columns of zeros and ones for each class value associated with every nominal attribute.  If only one attribute is used for input, then the number of columns is equal to the number of classes for that attribute.  If more columns appear in the data, then each nominal attribute is associated with several columns, one for each of its classes.

Each column consists of zeros, if that classification is not associated with this case, otherwise, one if that classification is associated.  Consider an example with one nominal variable and two classes: male and female (male, male, female, male, female).  With binary encoding, the following matrix is sent to the training engine to represent this data:

Continuous input and output data are passed to the training engine using two double precision arrays: continuous and outputs.  The number of rows in each of these matrices is n_patterns.  The number of columns in continuous and outputs, corresponds to the number of input and output variables, respectively.

Network Configuration

The configuration of the network consists of a description of the number of perceptrons for each layer, the number of hidden layers, the number of inputs and outputs, and a description of the linkages among the perceptrons.  This description is passed into this forecast routine through the structure Imsls_f_NN_Network.  See imsls_f_mlff_network.

Forecast Calculation

The forecast is calculated from the input attributes, network structure and weights provided in the structure Imsls_f_NN_Network.

Example

This example trains a two-layer network using 90 training patterns from one nominal and one continuous input attribute.  The nominal attribute has three classifications which are encoded using binary encoding.  This results in three binary network input columns.  The continuous input attribute is scaled to fall in the interval [0,1].

The network training targets were generated using the relationship:

Y = 10*X1 + 20*X2 + 30*X3 + 20*X4,

where X1, X2, X3 are the three binary columns, corresponding to the categories 1-3 of the nominal attribute, and X4 is the scaled continuous attribute.

The structure of the network consists of four input nodes ands two layers, with three perceptrons in the hidden layer and one in the output layer.  The following figure illustrates this structure:

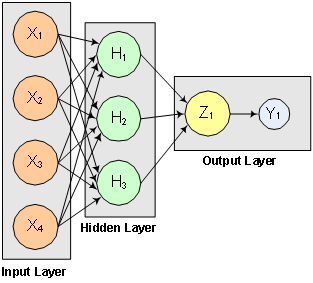
Figure 13- 13:  A 2-layer, Feedforward Network with 4 Inputs and 1 Output

There are a total of 100 outputs.  The first 90 outputs use imsls mlff_network_trainer to train the network and the last 10  outputs use imsls_mlff_network_forecast to forcast and compare the actual outputs.

 

#include <imsls.h>

#include <stdio.h>

int main ()

{

      int nominal[300] = {

      1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0,

      0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1,

      0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0,

      1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0,

      0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1,

      0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0,

      0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1,

      0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0,

      1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0,

      0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0,

      1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0,

      0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1,

      0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0,

      1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0,

      0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1

   };

      float continuous[100] = {

      4.007054658, 7.10028447, 4.740350984, 5.714553211, 6.205437459,

      2.598930065, 8.65089967, 5.705787357, 2.513348184, 2.723795955,

      4.1829356, 1.93280416, 0.332941608, 6.745567628, 5.593588463,

      7.273544478, 3.162117939, 4.205381208, 0.16414745, 2.883418275,

      0.629342241, 1.082223406, 8.180324708, 8.004894314, 7.856215418,

      7.797143157, 8.350033996, 3.778254431, 6.964837082, 6.13938006,

      0.48610387, 5.686627923, 8.146173848, 5.879852653, 4.587492779,

      0.714028533, 7.56324211, 8.406012623, 4.225261454, 6.369220241,

      4.432772218, 9.52166984, 7.935791508, 4.557155333, 7.976015058,

      4.913538616, 1.473658514, 2.592338905, 1.386872932, 7.046051685,

      1.432128376, 1.153580985, 5.6561491, 3.31163251, 4.648324851,

      5.042514515, 0.657054195, 7.958308093, 7.557870384, 7.901990083,

      5.2363088, 6.95582150, 8.362167045, 4.875903563, 1.729229471,

      4.380370223, 8.527875685, 2.489198107, 3.711472959, 4.17692681,

      5.844828801, 4.825754155, 5.642267843, 5.339937786, 4.440813223,

      1.615143829, 7.542969339, 8.100542684, 0.98625265, 4.744819569,

      8.926039258, 8.813441887, 7.749383991, 6.551841576, 8.637046998,

      4.560281415, 1.386055087, 0.778869034, 3.883379045, 2.364501589,

      9.648737525, 1.21754765, 3.908879368, 4.253313879, 9.31189696,

      3.811953836, 5.78471629, 3.414486452, 9.345413015, 1.024053777

   };

      float output[100] = {

      18.01410932, 24.20056894, 19.48070197, 21.42910642, 22.41087492,

      15.19786013, 27.30179934, 21.41157471, 15.02669637, 15.44759191,

      18.3658712, 13.86560832, 10.66588322, 23.49113526, 21.18717693,

      24.54708896, 16.32423588, 18.41076242, 10.3282949, 15.76683655,

      11.25868448, 12.16444681, 26.36064942, 26.00978863, 25.71243084,

      25.59428631, 26.70006799, 17.55650886, 23.92967416, 22.27876012,

      10.97220774, 21.37325585, 26.2923477, 21.75970531, 19.17498556,

      21.42805707, 35.12648422, 36.81202525, 28.45052291, 32.73844048,

      28.86554444, 39.04333968, 35.87158302, 29.11431067, 35.95203012,

      29.82707723, 22.94731703, 25.18467781, 22.77374586, 34.09210337,

      22.86425675, 22.30716197, 31.3122982, 26.62326502, 29.2966497,

      30.08502903, 21.31410839, 35.91661619, 35.11574077, 35.80398017,

      30.4726176, 33.91164302, 36.72433409, 29.75180713, 23.45845894,

      38.76074045, 47.05575137, 34.97839621, 37.42294592, 38.35385362,

      41.6896576, 39.65150831, 41.28453569, 40.67987557, 38.88162645,

      33.23028766, 45.08593868, 46.20108537, 31.9725053, 39.48963914,

      47.85207852, 47.62688377, 45.49876798, 43.10368315, 47.274094,

      39.1205628, 32.77211017, 31.55773807, 37.76675809, 34.72900318,

      49.29747505, 32.4350953, 37.81775874, 38.50662776, 48.62379392,

      37.62390767, 41.56943258, 36.8289729, 48.69082603, 32.04810755

   };

 

   /* 2D Array Definitions */

#define NOMINAL(i,j) nominal[i*n_nominal+j]

#define NOMINALOBS(i,j) nominalObs[i*n_nominal+j]

 

   Imsls_f_NN_Network *network;

 

   float *stats;

   int n_patterns = 100, n_nominal = 3, n_continuous = 1;

   int i, j, k, wIdx;

   float *forecasts;

   /*  for forecasting */

   int nominalObs[3] = { 0, 0, 0 };

   float continuousObs[1] = { 0 };

   float x, y;

   float *cont;

 

   /* Scale continuous attribute to the interval [0, 1] */

   cont = imsls_f_scale_filter (n_patterns, continuous, 1,

      IMSLS_SCALE_LIMITS, 0.0, 10.0, 0.0, 1.0, 0);

 

   network = imsls_f_mlff_network_init (4, 1);

 

   imsls_f_mlff_network (network,

      IMSLS_CREATE_HIDDEN_LAYER, 3, IMSLS_LINK_ALL, 0);

 

   for (j=network->n_inputs; j < network->n_nodes ; j++)

   {

      for (k=0; k < network->nodes[j].n_inLinks; k++)

      {

         wIdx = network->nodes[j].inLinks[k];

         /*   set specific layer weights */

         if (network->nodes[j].layer_id == 1) {

            network->links[wIdx].weight = 0.25;

         } else if (network->nodes[j].layer_id == 2) {

            network->links[wIdx].weight = 0.33;

         }

      }

   }

 

   imsls_random_seed_set (12345);

   stats = imsls_f_mlff_network_trainer (network, n_patterns - 10,

      n_nominal, n_continuous, nominal, continuous, output,

      0);

 

   printf ("Predictions for Observations 90 to 100: \n");

 

   for (i = 90; i < 100; i++)

   {

      continuousObs[0] = continuous[i];

      for (j = 0; j < n_nominal; j++)

      {

         NOMINALOBS (0, j) = NOMINAL (i, j);

      }

 

      forecasts = imsls_f_mlff_network_forecast (network, n_nominal,

         n_continuous, nominalObs, continuousObs, 0);

 

      x = output[i];

      y = forecasts[0];

      printf("observation[%d] %8.4f    Prediction %8.4f    ", i, x, y);

      printf("Residual %8.4f \n", x - y);

 

   }

 

   imsls_f_mlff_network_free (network);

#undef NOMINAL

#undef NOMINALOBS

}

 

Output

Predictions for Observations 90 to 100:

observation[90]  49.2975    Prediction  49.1823    Residual   0.1152

observation[91]  32.4351    Prediction  32.4410    Residual  -0.0059

observation[92]  37.8178    Prediction  37.7998    Residual   0.0179

observation[93]  38.5066    Prediction  38.4955    Residual   0.0111

observation[94]  48.6238    Prediction  48.5475    Residual   0.0763

observation[95]  37.6239    Prediction  37.6043    Residual   0.0196

observation[96]  41.5694    Prediction  41.5935    Residual  -0.0241

observation[97]  36.8290    Prediction  36.8038    Residual   0.0251

observation[98]  48.6908    Prediction  48.6110    Residual   0.0798

observation[99]  32.0481    Prediction  32.0631    Residual  -0.0150

---

Contact Support