Evaluates the inverse of the noncentral beta cumulative distribution function (CDF).
Synopsis
#include <imsls.h>
float imsls_f_non_central_beta_inverse_cdf (float p, float shape1, float shape2, float lambda)
The type double function is imsls_d_non_central_beta_inverse_cdf.
Required Arguments
float p
(Input)
Probability for which the inverse of the noncentral beta cumulative
distribution function is to be evaluated. p must be non-negative
and less than or equal to 1.
float shape1
(Input)
First shape parameter of the noncentral beta
distribution.
shape1 must be
positive.
float shape2
(Input)
Second shape parameter of the noncentral beta
distribution.
shape2 must be
positive.
float lambda
(Input)
Noncentrality parameter. lambda must be
non-negative.
Return Value
If the probability that a noncentral beta random variable takes a value less than or equal to x is p, then x is the return value of the noncentral beta inverse CDF evaluated at p.
Description
The noncentral beta distribution is a generalization of the beta distribution. If Z is a noncentral chi-square random variable with noncentrality parameter λ and 2α1 degrees of freedom, and Y is a chi-square random variable with 2α2 degrees of freedom which is statistically independent of Z, then
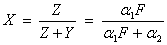
is a noncentral beta-distributed random variable and
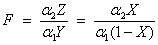
is a noncentral F-distributed random variable. The CDF for noncentral beta variable X can thus be simply defined in terms of the noncentral F CDF:
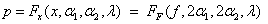
where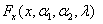 
is a noncentral beta CDF with
x = x,
α1= shape1,
α2 = shape2,
and noncentrality parameter λ = lambda;
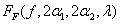is a noncentral F CDF with
argument f , numerator and denominator degrees of freedom 2α1
and 2α2 respectively, and noncentrality parameter
λ; p = the probability that
F < f = the probability that
X < x; and
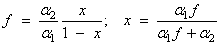
(See documentation for function imsls_f_non_central_F_cdf for a discussion of how the noncentral F CDF is defined and calculated.) The correspondence between the arguments of function imsls_f_non_central_beta_inverse_cdf and the variables in the above equations is as follows: α1 = shape1, α2 = shape2, λ = lambda, and p = p.
Function imsls_f_non_central_beta_inverse_cdf evaluates
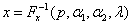
by first evaluating
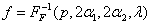
and then solving for x using
.
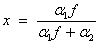(See documentation for function imsls_f_non_central_F_inverse_cdf for a discussion of how the inverse noncentral F CDF is calculated.)
Example
This example traces out a portion of an inverse noncentral beta distribution with parameters shape1 = 50, shape2 = 5, and lambda = 10.
#include <imsls.h>
#include <stdio.h>
int main()
{
int i;
float f[] = {0.0, 0.4, 0.8, 1.2, 1.6, 2.0, 2.8, 4.0};
float shape1 = 50., shape2 = 5., lambda =10.;
float x, p, bcdfinv;
printf ("shape1: %4.0f\n", shape1);
printf ("shape2: %4.0f\n", shape2);
printf ("lambda: %4.0f\n\n", lambda);
printf (" x p = cdf(x) cdfinv(p)\n");
for (i=0; i<8; i++) {
x = (shape1*f[i]) / (shape1*f[i] + shape2);
p = imsls_f_non_central_beta_cdf
(x, shape1, shape2, lambda);
bcdfinv = imsls_f_non_central_beta_inverse_cdf
(p, shape1, shape2, lambda);
printf (" %12.4e %12.4e %12.4e\n", x, p, bcdfinv);
}
}
Output
shape1: 50
shape2: 5
lambda: 10
x p = cdf(x) cdfinv(p)
0.0000e+000 0.0000e+000 0.0000e+000
8.0000e-001 4.8879e-003 8.0000e-001
8.8889e-001 2.0263e-001 8.8889e-001
9.2308e-001 5.2114e-001 9.2308e-001
9.4118e-001 7.3385e-001 9.4118e-001
9.5238e-001 8.5041e-001 9.5238e-001
9.6552e-001 9.4713e-001 9.6552e-001
9.7561e-001 9.8536e-001 9.7561e-001
