Evaluates the noncentral chi-squared probability density function.
Synopsis
float imsls_f_non_central_chi_sq_pdf (float x, float df, float lambda)
The type double function is imsls_d_non_central_chi_sq_pdf.
Required Arguments
float x
(Input)
Argument for which the noncentral chi-squared probability
density function is to be evaluated. x must be greater than or equal to 0.
float df
(Input)
Number of degrees of freedom of the noncentral chi-squared
distribution.
df must be greater than 0.
float lambda
(Input)
Noncentrality parameter. lambda must be greater than or equal to 0.
Return Value
The probability density associated with a noncentral chi-squared random variable with value x.
Description
The noncentral chi-squared distribution is a generalization of the chi-squared distribution. If {Xi} are k independent, normally distributed random variables with means μi and variances σ2i, then the random variable:
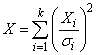
is distributed according to the noncentral chi-squared distribution. The noncentral chi-squared distribution has two parameters: k which specifies the number of degrees of freedom (i.e. the number of Xi), and λ which is related to the mean of the random variables Xi by:
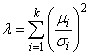
The noncentral chi-squared distribution is equivalent to a (central) chi-squared distribution with k + 2i degrees of freedom, where i is the value of a Poisson distributed random variable with parameter λ ∕ 2. Thus, the probability density function is given by:
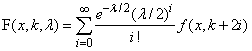
where the (central) chi-squared PDF f(x, k) is given by:
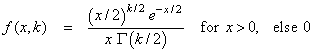
where Γ(.) is the gamma function. The above representation of F(x, k, λ) can be shown to be equivalent to the representation:
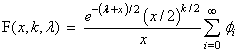
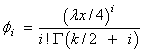
Function imsls_f_non_central_chi_sq_pdf evaluates the probability density function of a noncentral chi-squared random variable with df degrees of freedom and noncentrality parameter lambda, corresponding to k = df, λ = lambda, and x = x.
Function imsls_f_non_central_chi_sq evaluates the cumulative distribution function incorporating the above probability density function.
With a noncentrality parameter of zero, the noncentral chi-squared distribution is the same as the central chi-squared distribution.
Example
This example calculates the noncentral chi-squared distribution for a distribution with 100 degrees of freedom and noncentrality parameter λ = 40.
#include <imsls.h>
#include <stdio.h>
int main()
{
int i;
float x[] = {0, 8, 40, 136, 280, 400};
float df = 100, lambda = 40.0, pdfv;
printf ("\n\n df: %4.0f; lambda: %4.0f\n\n",
df, lambda);
printf (" x pdf(x)\n");
for (i=0; i<6; i++) {
pdfv = imsls_f_non_central_chi_sq_pdf(x[i], df, lambda);
printf (" %5.0f %12.4e\n",x[i], pdfv);
}
}
Output
df: 100; lambda: 40
x pdf(x)
0 0.0000e+000
8 4.7644e-044
40 3.4621e-014
136 2.1092e-002
280 4.0027e-010
400 1.1250e-022
