Evaluates the inverse of the noncentral Student’s t distribution function.
Synopsis
#include <imsls.h>
float imsls_f_non_central_t_inv_cdf (float p, int df , float delta)
The type double function is imsls_d_non_central_t_inv_cdf.
Required Arguments
float
p
(Input)
A
Probability for which the inverse of the noncentral Student’s t
distribution function is to be evaluated. p must be in the
open interval (0.0, 1.0).
int
df
(Input)
Number
of degrees of freedom of the noncentral Student’s t distribution.
Argument df must be greater
than or equal to 0.0
float
delta
(Input)
The
noncentrality parameter.
Return Value
The probability that a noncentral Student’s t random variable takes a value less than or equal to t is p.
Description
Function imsls_f_non_central_t_inv_cdf evaluates the inverse distribution function of a noncentral t random variable with df degrees of freedom and noncentrality parameter delta; that is, with P = p, v = df, and δ = delta, it determines t0 (= imsls_f_non_central_t_inv_cdf (p, df, delta)), such that
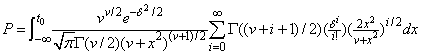
where Γ(⋅) is the gamma function. The probability that the random variable takes a value less than or equal to t0 is P. See imsls_f_non_central_t_cdf for an alternative definition in terms of normal and chi-squared random variables. The function imsls_f_non_central_t_inv_cdf uses bisection and modified regula falsi to invert the distribution function, which is evaluated using function imsls_f_non_central_t_cdf.
Example
In this example, we find the 95-th percentage point for a noncentral t random variable with 6 degrees of freedom and noncentrality parameter 6.
#include <imsls.h>
#include <stdio.h>
int main()
{
int df = 6;
float p = 0.95, delta = 6.0, t;
t = imsls_f_non_central_t_inv_cdf(p, df, delta);
printf("The %4.2f noncentral t critical value is "
"%6.4f.\n", 1.0-p, t);
}
Output
The 0.05 noncentral t critical value is 11.995.
