Fits data to a nonlinear model (possibly with linear constraints) using the successive quadratic programming algorithm (applied to the sum of squared errors, sse = Σ(y_i − f(x_i; θ))²) and either a finite difference gradient or a user-supplied gradient.

Synopsis

#include <imsls.h>

float *imsls_f_nonlinear_optimization (float fcn(), int n_parameters, int n_observations, int n_independent, float x[], float y[], ..., 0)

The type double function is imsls_d_nonlinear_optimization.

Required Arguments

float fcn (int n_independent, float xi[], int n_parameters, float theta[])
User-supplied function to evaluate the function that defines the nonlinear regression problem where xi is an array of length n_independent at which point the function is evaluated and theta is an array of length n_parameters containing the current values of the regression coefficients. Function fcn returns a predicted value at the point xi. In the following, f(x_i; θ), or just f_i, denotes the value of this function at the point x_i, for a given value of θ. (Both x_i and θ are arrays.)

int n_parameters   (Input)
Number of parameters to be estimated.

int n_observations   (Input)
Number of observations.

int n_independent   (Input)
Number of independent variables.

float *x   (Input)
Array of size n_observations by n_independent containing the matrix of inde­pendent (explanatory) variables.

float y[]   (Input)
Array of length n_observations containing the dependent (response) variable.

Return Value

A pointer to an array of length n_parameters containing a solution, 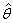 for the nonlinear regression coefficients. To release this space, use imsls_free. If no solution can be computed, then NULL is returned.

Synopsis with Optional Arguments

#include <imsls.h>

float *imsls_f_nonlinear_optimization (float fcn(), int n_parameters, int n_observations, int n_independent, float x[], float y[],

IMSLS_THETA_GUESS, float theta_guess[],

IMSLS_JACOBIAN, void jacobian(),

IMSLS_SIMPLE_LOWER_BOUNDS, float theta_lb[],

IMSLS_SIMPLE_UPPER_BOUNDS, float theta_ub[],

IMSLS_LINEAR_CONSTRAINTS, int n_constraints, int n_equality, float a[], float b[],

IMSLS_FREQUENCIES, float frequencies,

IMSLS_WEIGHTS, float weights,IMSLS_ACC, float acc,

IMSLS_MAX_SSE_EVALUATIONS, int *max_sse_eval,

IMSLS_PRINT_LEVEL, int print_level,

IMSLS_STOP_INFO, int *stop_info,

IMSLS_ACTIVE_CONSTRAINTS_INFO, int *n_active, int **indices_active, float **multiplier,

IMSLS_ACTIVE_CONSTRAINTS_INFO_USER, int *n_active, int indices_active[], float multiplier[],

IMSLS_PREDICTED, float **predicted,

IMSLS_PREDICTED_USER, float predicted[],

IMSLS_RESIDUAL, float **residual,

IMSLS_RESIDUAL_USER, float residual[],

IMSLS_SSE, float *sse,

IMSLS_RETURN_USER, float theta_hat[],

IMSLS_FCN_W_DATA, float fcn(), void *data,

IMSLS_JACOBIAN_W_DATA, float jacobian(), void *data,

0)

Optional Arguments

IMSLS_THETA_GUESS, float theta_guess[]   (Input)
Array with n_parameters components containing an initial guess.
Default: theta_guess[] = 0

IMSLS_JACOBIAN, void jacobian (int n_independent, float xi[], int n_parameters, float theta[], float fjac[])   (Input/Output)
User-supplied function to compute the i-th row of the Jacobian, where the n_independent data values corresponding to the i-th row are input in xi. Argument theta is an array of length n_parameters containing the regression coefficients for which the Jacobian is evaluated, fjac is the computed n_parameters row of the Jacobian for observation i at theta. Note that each derivative f(x_i)∕θ should be returned in fjac[j-1] for i = 1, 2, ..., n_parameters. Further note that in order to maintain consistency with the other nonlinear solver, nonlinear_regression, the Jacobian values must be specified as the negative of the calculated derivatives.

IMSLS_SIMPLE_LOWER_BOUNDS, float theta_lb[]   (Input)
Vector of length n_parameters containing the lower bounds on the parameters; choose a very large negative value if a component should be unbounded below or set theta_lb[i] = theta_ub[i] to freeze the i-th variable.
Default: All parameters are bounded below by -10⁶.

IMSLS_SIMPLE_UPPER_BOUNDS, float theta_ub[]   (Input)
Vector of length n_parameters containing the upper bounds on the parameters; choose a very large value if a component should be unbounded above or set theta_lb[i] = theta_ub[i] to freeze the i-th variable.
Default: All parameters are bounded above by 10⁶.

IMSLS_LINEAR_CONSTRAINTS, int n_constraints, int n_equality, float a[], float b[]   (Input)
Argument n_constraints is the total number of linear constraints (excluding simple bounds). Argument n_equality is the number of these constraints which are equality constraints; the remaining n_constraints − n_equality constraints are inequality constraints. Argument a is a n_constraints by n_parameters array containing the equality constraint gradients in the first n_equality rows, followed by the ine­quality constraint gradients. Argument b is a vector of length n_constraints containing the right-hand sides of the linear constraints.

            Specifically, the constraints on θ are:

            a_i1 θ₁ + ... + a_ij θ_j = b_i   for i = 1, n_equality and j = 1, n_parameter, and

            a_k1 θ₁ + ... + a_kj θ_j ≤ b_k   for k = n_equality + 1, n_constraints and j = 1, n_parameter.

            Default: There are no default linear constraints.

IMSLS_FREQUENCIES, float frequencies[]   (Input)
Array of length n_observations containing the frequency for each observation.
Default: frequencies[] = 1

IMSLS_WEIGHTS, float weights[]   (Input)
Array of length n_observations containing the weight for each observation.
Default: weights[] = 1

IMSLS_ACC, float acc   (Input)
The nonnegative tolerance on the first order conditions at the calculated solution.

IMSLS_MAX_SSE_EVALUATIONS, int *max_sse_eval   (Input/Output)
On input max_sse_eval is the maximum number of sse evaluations allowed. On output, max_sse_eval contains the actual number of sse evaluations needed.
Default: max_sse_eval = 400

IMSLS_PRINT_LEVEL, int print_level   (Input)
Argument print_level specifies the frequency of printing during execution. If print_level = 0, there is no printing. Otherwise, after ensuring feasibility, informa­tion is printed every print_level iterations and whenever an internal tolerance (called tol) is reduced. The printing provides the values of theta and the sse and gradient at the value of theta. If print_level is negative, this information is augmented by the current values of indices_active, multiplier, and reskt, where reskt is the Kuhn-Tucker residual vector at theta.

IMSLS_STOP_INFO, int *stop_info   (Output)
Argument stop_info will have one of the following integer values to indicate the rea­son for leaving the routine:

 

stop_info	Reason for leaving routine
1	θ is feasible, and the condition that depends on acc is sat­isfied.
2	θ is feasible, and rounding errors are preventing further progress.
3	θ is feasible, but sse fails to decrease although a decrease is predicted by the current gradient vector.
4	The calculation cannot begin because a contains fewer than n_constraints constraints or because the lower bound on a variable is greater than the upper bound.
5	The equality constraints are inconsistent. These constraints include any components of that are frozen by setting theta_lb[i] equal to theta_ub[i].
6	The equality constraints and the bound on the variables are found to be inconsistent.
7	There is no possible θ that satisfies all of the constraints.
8	Maximum number of sse evaluations (max_sse_eval) is exceeded.
9	θ is determined by the equality constraints.

 

IMSLS_ACTIVE_CONSTRAINTS_INFO, int *n_active, int **indices_active, float **multiplier   (Output)
Argument n_active returns the final number of active constraints. Argument indices_active is the address of a pointer to an internally allocated integer array of length n_active containing the indices of the final active constraints. Argument multiplier is the address of a pointer to an internally allocated real array of length n_active containing the Lagrange multiplier estimates of the final active constraints.

IMSLS_ACTIVE_CONSTRAINTS_INFO_USER, int *n_active, int indices_active[], float multiplier[]   (Output)
Storage for arrays indices_active and multiplier are provided by the user. The maximum length needed for these arrays is n_constraints. See IMSLS_ACTIVE_CONSTRAINTS_INFO.

IMSLS_PREDICTED, float **predicted   (Output)
Address of a pointer to a real internally allocated array of length n_observations containing the predicted values at the approximate solution.

IMSLS_PREDICTED_USER, float predicted[]   (Output)
Storage for array predicted is provided by the user. See IMSLS_PREDICTED.

IMSLS_RESIDUAL, float **residual   (Output)
Address of a pointer to a real internally allocated array of length n_observations containing the residuals at the approximate solution.

IMSLS_RESIDUAL_USER, float residual[]   (Output)
Storage for array residual is provided by the user. See IMSLS_RESIDUAL.

IMSLS_SSE, float *sse   (Output)
Residual sum of squares.

IMSLS_RETURN_USER, float theta_hat[]   (Output)
User-allocated array of length n_parameters containing the estimated regression coefficients.

IMSLS_FCN_W_DATA, float fcn (int n_independent, float xi[],int n_parameters, float theta[]), void *data, (Input)
User-supplied function to evaluate the function that defines the nonlinear regression problem, which also accepts a pointer to data that is supplied by the user.  data is a pointer to the data to be passed to the user-supplied function.  See the “Introduction, Passing Data to User-Supplied Functions” at the beginning of this manual for more details.

IMSLS_JACOBIAN_W_DATA, void jacobian (int n_independent, float xi[], int n_parameters, float theta[], float fjac[]), void *data, (Input)
User-supplied function to compute the i-th row of the Jacobian, which also accepts a pointer to data that is supplied by the user.  data is a pointer to the data to be passed to the user-supplied function.  See the “Introduction, Passing Data to User-Supplied Functions” at the beginning of this manual for more details.

Description

Function imsls_f_nonlinear_optimization is based on M.J.D. Powell’s TOLMIN, which solves linearly constrained optimization problems, i.e., problems of the form min f(θ), θ ∈ ℜ, subject to

A₁θ = b₁

A₂θ ≤ b₂

θ_I ≤ θ ≤ θ_u

given the vectors b₁,  b₂, θ_I, and θ_u and the matrices A₁ and A₂.

The algorithm starts by checking the equality constaints for inconsistency and redundancy. If the equality constraints are consistent, the method will revise θ⁰, the initial guess provided by the user, to satisfy

A₁θ = b₁

Next, θ⁰ is adjusted to satisfy the simple bounds and inequality constraints. This is done by solv­ing a sequence of quadratic programming subproblems to minimize the sum of the constraint or bound violations.

Now, for each iteration with a feasible θ^k, let J_k be the set of indices of inequality constraints that have small residuals. Here, the simple bounds are treated as inequality constraints. Let I_k be the set of indices of active constraints. The following quadratic programming problem

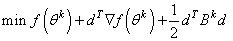
subject to

a_jd = 0    j ∈ I_k

a_jd ≤ 0   j ∈ J_k

is solved to get (d^k, λ^k) where a_j is a row vector representing either a constraint in A₁ or A₂ or a bound constraint on θ. In the latter case, the a_j = e_i for the bound constraint θ_i ≤ (θ_u)_i and a_j = −e_i for the constraint θ_i ≤ (θ_l)_i. Here, e_i is a vector with a 1 as the i-th component, and zeroes elsewhere. λ^k are the Lagrange multipliers, and B^k is a positive definite approximation to the second derivative ∇² f(θ^k).

After the search direction d^k is obtained, a line search is performed to locate a better point. The new point θ^k+1 = θ^k + α^kd^k has to satisfy the conditions

f (θ^k + α^kd^k) ≤ f (θ^k) + 0.1α^k (d^k)^T∇ f (θ^k)

and

(d^k)^T∇ f (θ^k + α^kd^k) ≥ 0.7 (d^k)^T∇ f (θ^k)

The main idea in forming the set J_k is that, if any of the inequality constraints restricts the step-length α^k, then its index is not in J_k. Therefore, small steps are likely to be avoided.

Finally, the second derivative approximation, B^k, is updated by the BFGS formula, if the condition

(d^k)^T∇ f (θ^k + α^kd^k) − ∇ f (θ^k) > 0

holds. Let θ^k ← θ^k+1, and start another iteration.

The iteration repeats until the stopping criterion

||∇ f (θ^k) − A^kλ^k||₂ ≤ τ

is satisfied; here, τ is a user-supplied tolerance. For more details, see Powell (1988, 1989).

Since a finite-difference method is used to estimate the gradient for some single precision cal­culations, an inaccurate estimate of the gradient may cause the algorithm to terminate at a noncritical point. In such cases, high precision arithmetic is recommended. Also, whenever the exact gradient can be easily provided, the gradient should be passed to imsls_f_nonlinear_optimization using the optional argument IMSLS_JACOBIAN.

Examples

Example 1

In this example, a data set is fitted to the nonlinear model function

 

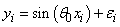
#include <imsls.h>

#include <math.h>

float fcn(int n_independent, float x[], int n_parameters, float theta[]);

int main()

{

    int     n_parameters   =  1;

    int     n_observations = 11;

    int     n_independent  =  1;

    float   *theta_hat;

    float   x[11] = {0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6,

                     0.7, 0.8, 0.9, 1.0};

    float   y[15] = {0.05, 0.21, 0.67, 0.72, 0.98, 0.94,

                     1.00, 0.73, 0.44, 0.36, 0.02};

    imsls_omp_options(IMSLS_SET_FUNCTIONS_THREAD_SAFE, 1, 0);

 

    theta_hat =

        imsls_f_nonlinear_optimization(fcn, n_parameters,

                                       n_observations, n_independent, x, y,

                                       0);

    imsls_f_write_matrix("Theta Hat", 1, n_parameters, theta_hat, 0);

    imsls_free(theta_hat);

}

float fcn(int n_independent, float x[], int n_parameters, float theta[])

{

   return sin(theta[0]*x[0]);

}

Output

 

 Theta Hat

     3.161

Example 2

Draper and Smith (1981, p. 475) state a problem due to Smith and Dubey. [H. Smith and S. D. Dubey (1964), "Some reliability problems in the chemical industry", Industrial Quality Control, 21 (2), 1964, pp. 64−70] A certain product must have 50% available chlorine at the time of manufacture. When it reaches the customer 8 weeks later, the level of available chlorine has dropped to 49%. It was known that the level should stabilize at about 30%. To predict how long the chemical would last at the customer site, samples were analyzed at different times. It was postulated that the following nonlinear model should fit the data.

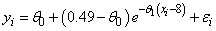
Since the chlorine level will stabilize at about 30%, the initial guess for theta1 is 0.30. Using the last data point (x = 42, y = 0.39) and θ0 = 0.30 and the above nonlinear equation, an estimate for θ1of 0.02 is obtained.

The constraints that θ0 ≥ = 0 and θ1 ≥ = 0 are also imposed. These are equivalent to requiring that the level of available chlorine always be positive and never increase with time.

The Jacobian of the nonlinear model equation is also used.

 

#include <imsls.h>

#include <math.h>

float fcn(int n_independent, float x[], int n_parameters, float theta[]);

void jacobian(int n_independent, float x[], int n_parameters,

              float theta[], float fjac[]);

int main()

{

    int     n_parameters   =  2;

    int     n_observations = 44;

    int     n_independent  =  1;

    float   *theta_hat;

    float   x[44] = {

        8.0, 8.0, 10.0, 10.0, 10.0, 10.0, 12.0, 12.0, 12.0,

        12.0, 14.0, 14.0, 14.0, 16.0, 16.0, 16.0, 18.0, 18.0, 20.0,

        20.0, 20.0, 22.0, 22.0, 22.0, 24.0, 24.0, 24.0, 26.0, 26.0,

        26.0, 28.0, 28.0, 30.0, 30.0, 30.0, 32.0, 32.0, 34.0, 36.0,

        36.0, 38.0, 38.0, 40.0, 42.0};

    float   y[44] = {

        .49, .49, .48, .47, .48, .47, .46, .46, .45, .43, .45,

        .43, .43, .44, .43, .43, .46, .45, .42, .42, .43, .41, .41,

        .4, .42, .4, .4, .41, .4, .41, .41, .4, .4, .4, .38, .41,

        .4, .4, .41, .38, .4, .4, .39, .39};

    float   guess[2] =  {0.30, 0.02};

    float   xlb[2] = {0.0, 0.0};

    float   sse;

    imsls_omp_options(IMSLS_SET_FUNCTIONS_THREAD_SAFE, 1, 0);

 

    theta_hat =

        imsls_f_nonlinear_optimization(fcn, n_parameters, n_observations,

                                       n_independent, x, y,

                                       IMSLS_THETA_GUESS, guess,

                                       IMSLS_SIMPLE_LOWER_BOUNDS, xlb,

                                       IMSLS_JACOBIAN, jacobian,

                                       IMSLS_SSE, &sse,

                                       0);

    imsls_f_write_matrix("Theta Hat", 1, 2, theta_hat, 0);

    imsls_free(theta_hat);

}

float fcn(int n_independent, float x[], int n_parameters, float theta[])

{

    return  theta[0] + (0.49-theta[0])*exp(-theta[1]*(x[0]-8.0));

}

 

 

void jacobian(int n_independent, float x[], int n_parameters,

              float theta[],

float fjac[])

{

    fjac[0] = -1.0 + exp(-theta[1]*(x[0]-8.0));

    fjac[1] = (0.49-theta[0])*(x[0]-8.0) * exp(-theta[1]*(x[0]-8.0));

}

Output

 

       Theta Hat

         1           2

    0.3901      0.1016

Fatal Errors

 

IMSLS_BAD_CONSTRAINTS_1	The equality constraints are inconsistent.
IMSLS_BAD_CONSTRAINTS_2	The equality constraints and the bounds on the vari­ables are found to be inconsistent.
IMSLS_BAD_CONSTRAINTS_3	No vector “theta” satisfies all of the constraints. Specifically, the current active constraints prevent any change in “theta” that reduces the sum of constraint violations.
IMSLS_BAD_CONSTRAINTS_4	The variables are determined by the equality constraints.
IMSLS_TOO_MANY_ITERATIONS_1	Number of function evaluations exceeded “maxfcn” = #.

 

---

Contact Support