Generates pseudorandom numbers from a multinomial distribution.
Synopsis
#include <imsls.h>
int
*imsls_random_multinomial (int
n_random,
int
n,
int
k,
float
p[],
..., 0)
Required Arguments
int n_random
(Input)
Number of random multinomial vectors
to generate.
int n
(Input)
Multinomial parameter indicating the
number of independent trials.
int k
(Input)
The number of mutually exclusive outcomes
on any trial. k is the length of the multinomial vectors. k must be greater than or equal to
2.
float p[]
(Input)
Vector of length k containing the probabilities of the possible outcomes. The
elements of p must be positive and must sum to
1.0.
Return Value
n_random by k matrix containing the random multinomial vectors in its rows. To release this space, use free.
Synopsis with Optional Arguments
#include <imsls.h>
int
*imsls_random_multinomial (int
n_random,
int
n,
int
k,
float
p[],
IMSLS_RETURN_USER,
float
r[],
0)
Optional Arguments
IMSLS_RETURN_USER, float r[]
(Output)
User-supplied array of length n_random × k containing the
random deviates.
Description
Function imsls_random_multinomial generates pseudorandom numbers from a K-variate multinomial distribution with parameters n and p. k and n must be positive. Each element of p must be positive and the elements must sum to 1. The probability function (with n = n, k = k, and pi = p[i+1]) is
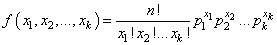
for xi ≥ 0 and
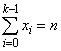
The deviate in each row of r is produced by generation of the binomial deviate x0 with parameters n and pi and then by successive generations of the conditional binomial deviates xj given x0, x1, …, xj−2 with parameters n − x0 − x1 − … − xj−2 and pj /(1 − p0 - p1 − … −pj−2).
Example
In this example, imsls_random_multinomial is used to generate five pseudorandom 3-dimensional multinomial variates with parameters n = 20 and p = [0.1, 0.3, 0.6].
#include <stdio.h>
#include <imsls.h>
int main()
{
int nr = 5, n = 20, k = 3, *ir;
float p[3] = {.1, .3, .6};
imsls_random_seed_set(123457);
ir = imsls_random_multinomial(nr, n, k, p, 0);
imsls_i_write_matrix("Multinomial random_deviates", 5, 3, ir,
IMSLS_NO_ROW_LABELS,
IMSLS_NO_COL_LABELS, 0);
}
Output
Multinomial random_deviates
5 4 11
3 6 11
3 3 14
5 5 10
4 5 11
