Generates pseudorandom numbers from a nonhomogeneous Poisson process.
Synopsis
#include <imsls.h>
float
*imsls_f_random_npp (float
tbegin,
float
tend, float
ftheta(),
float
theta_min,
float
theta_max,
int
neub,
int *ne, ...,
0)
The type double function is imsls_d_random_npp.
Required Arguments
float tbegin
(Input)
Lower endpoint of the time interval of the
process.
tbegin must be nonnegative. Usually, tbegin = 0.
float tend
(Input)
Upper endpoint of the time interval of the
process.
tend must be greater than tbegin.
float
ftheta(float t)
(Input)
User-supplied function to provide the value of the rate of the
process as a function of time. This function must be defined over the interval
from tbegin to
tend and must be
nonnegative in that interval.
float theta_min
(Input)
Minimum value of the rate function
ftheta() in the interval (tbegin, tend).
If the actual minimum is unknown, set
theta_min = 0.0.
float theta_max
(Input)
Maximum value of the rate function
ftheta() in the interval (tbegin, tend).
If the actual maximum is unknown, set theta_max to a known upper bound of the maximum. The efficiency of
imsls_f_random_npp is less the greater theta_max exceeds the true maximum.
int neub
(Input)
Upper bound on the number of events to be
generated.
In order to be reasonably sure that the full process through time
tend is generated, calculate neub as neub = X + 10.0 * SQRT(X), where
X = theta_max
*
(tend − tbegin).
int *ne
(Output)
Number of events
actually generated.
If ne is less that neub, the time tend is reached before neub events are realized.
Return Value
An array of length neub containing the the times to events in the first ne elements. To release this space, use free.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_random_npp (float
tbegin,
float
tend,
float
ftheta(),
float theta_min,
float
theta_max,
int
neub,
int *ne,
IMSLS_RETURN_USER,
float
r[],
IMSLS_FCN_W_DATA,
float
ftheta(),
void
*data,
0)
Optional Arguments
IMSLS_RETURN_USER, float r[]
(Output)
User-supplied array of length neub containing the
the times to events in the first ne elements.
IMSLS_FCN_W_DATA, float
ftheta(float t), void *data,
(Input)
User-supplied function to provide the value of the rate of the
process as a function of time, which also accepts a pointer to data that is
supplied by the user. data is a pointer to
the data to be passed to the user-supplied function. See the
“Introduction”, Passing Data
to User-Supplied Functions at the beginning of this manual for more
details.
Description
Function imsls_f_random_npp simulates a one-dimensional nonhomogeneous Poisson process with rate function ftheta in a fixed interval (tbegin, tend].
Let λ(t) be the rate function and t0 = tbegin and t1 = tend. Function imsls_f_random_npp uses a method of thinning a nonhomogeneous Poisson process {N*(t), t ≥ t0} with rate function λ*(t) ≥ λ(t) in (t0, t1], where the number of events, N*, in the interval (t0, t1] has a Poisson distribution with parameter
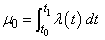
The function
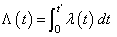
is called the integrated rate
function.) In imsls_f_random_npp, λ*(t) is taken to be a constant λ*(= theta_max) so that at time ti, the time of the next event
ti+1 is obtained by generating and cumulating exponential random
numbers
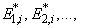
with parameter λ*, until for the first time
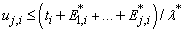
where the uj,i are independent uniform random numbers between 0 and 1. This process is continued until the specified number of events, neub, is realized or until the time, tend, is exceeded. This method is due to Lewis and Shedler (1979), who also review other methods. The most straightforward (and most efficient) method is by inverting the integrated rate function, but often this is not possible.
If theta_max is actually greater than the maximum of λ(t) in (t0, t1], the function will work, but less efficiently. Also, if λ(t) varies greatly within the interval, the efficiency is reduced. In that case, it may be desirable to divide the time interval into subintervals within which the rate function is less variable. This is possible because the process is without memory.
If no time horizon arises naturally, tend must be set large enough to allow for the required number of events to be realized. Care must be taken; however, that ftheta is defined over the entire interval.
After simulating a given number of events, the next event came be generated by setting tbegin to the time of the last event (the sum of the elements in R) and calling imsls_f_random_npp again. Cox and Lewis (1966) discuss modeling applications of nonhomogeneous Poisson processes.
Example
In this example, imsls_f_random_npp is used to generate the first five events in the time 0 to 20 (if that many events are realized) in a nonhomogeneous process with rate function
λ(t) = 0.6342 exp(0.001427t)
for 0 < t ≤ 20.
Since this is a monotonically increasing function of t, the minimum is at t = 0 and is 0.6342, and the maximum is at t = 20 and is 0.6342 exp(0.02854) = 0.652561.
#include <stdio.h>
#include <imsls.h>
int main()
{
float *r, tmax= .652561, tmin = .6342, tbeg=0., tend=20.;
imsls_random_seed_set(123457);
r = imsls_f_random_npp(tbeg, tend, ftheta, tmin, tmax, neub, &ne, 0);
printf("Inter-event times for the first %d events in the process:\n", ne);
for (i=0; i<ne; i++) printf("\t%f\n", r[i]);
}
float ftheta (float t)
}
return 0.6342*exp(0.001427*t);
}
Output
Inter-event times for the first 5 events in the process:
0.052660
0.407979
0.258399
0.019767
0.167641
