Selects the best multiple linear regression models.
Synopsis
#include <imsls.h>
void imsls_f_regression_selection (int n_rows, int n_candidate, float x[], float y[], ..., 0)
The type double function is imsls_d_regression_selection.
Required Arguments
int n_rows
(Input)
Number of observations or rows in x and y.
int
n_candidate (Input)
Number of candidate variables
(independent variables) or columns in x. n_candidate must be
greater than 2.
float x[]
(Input)
Array of size n_rows × n_candidate containing
the data for the candidate variables.
float y[]
(Input)
Array of length n_rows containing the
responses for the dependent variable.
Synopsis with Optional Arguments
#include <imsls.h>
void imsls_f_regression_selection (int n_rows, int n_candidate, float x[], float y[],
IMSLS_X_COL_DIM, int x_col_dim,
IMSLS_PRINT, or
IMSLS_NO_PRINT,
IMSLS_WEIGHTS, float weights[],
IMSLS_FREQUENCIES, float frequencies[],
IMSLS_R_SQUARED, int max_subset_size, or
IMSLS_ADJ_R_SQUARED, or
IMSLS_MALLOWS_CP,
IMSLS_MAX_N_BEST, int max_n_best,
IMSLS_MAX_N_GOOD_SAVED, int max_n_good_saved,
IMSLS_CRITERIONS, int **index_criterions, float **criterions,
IMSLS_CRITERIONS_USER, int index_criterions[], float criterions[],
IMSLS_INDEPENDENT_VARIABLES, int **index_variables, int **independent_variables,
IMSLS_INDEPENDENT_VARIABLES_USER, int index_variables[],int independent_variables[],
IMSLS_COEF_STATISTICS, int **index_coefficients,
IMSLS_COEF_STATISTICS_USER, int index_coefficients[],
IMSLS_INPUT_COV, int n_observations, float cov[],
0)
Optional Arguments
IMSLS_X_COL_DIM, int x_col_dim
(Input)
The column dimension of x.
Default: x_col_dim =
n_candidate
IMSLS_PRINT
Printing
is performed. This is the default.
or
IMSLS_NO_PRINT
Printing
is not performed.
IMSLS_WEIGHTS, float weights[]
(Input)
Array of length n_rows containing the
weight for each row of x.
Default: weights[] = 1
IMSLS_FREQUENCIES, float
frequencies[] (Input)
Array of length n_rows containing the
frequency for each row of x.
Default: frequencies[] = 1
IMSLS_R_SQUARED, int
max_subset_size (Input)
The R2 criterion is used, where subset sizes 1,
2, ..., max_subset_size are
examined. This option is the default with max_subset_size = n_candidate.
or
IMSLS_ADJ_R_SQUARED
The
adjusted R2 criterion is
used, where subset sizes 1, 2, ..., n_candidate are
examined.
or
IMSLS_MALLOWS_CP
Mallows
Cp criterion is used, where subset sizes 1, 2, ..., n_candidate are
examined.
IMSLS_MAX_N_BEST, int
max_n_best (Input)
Number of best regressions to be found.
If the R2 criterions are
selected, the max_n_best best
regressions for each subset size examined are found. If the adjusted
R2 or Mallows
Cp criterion is selected, the max_n_best overall
regressions are found.
Default: max_n_best = 1
IMSLS_MAX_N_GOOD_SAVED, int
max_n_good_saved (Input)
Maximum number of good
regressions of each subset size to be saved in finding the best regressions.
Argument max_n_good_saved must
be greater than or equal to max_n_best. Normally,
max_n_good_saved
should be less than or equal to 10. It doesn't ever need to be larger than the
maximum number of subsets for any subset size. Computing time required is
inversely related to max_n_good_saved.
Default:
max_n_good_saved
= 10
IMSLS_CRITERIONS, int
**index_criterions, float
**criterions (Output)
Argument index_criterions is
the address of a pointer to the internally allocated array of length
nsize + 1(where nsize is equal to max_subset_size if
optional argument IMSLS_R_SQUARED is
specified; otherwise, nsize is equal to n_candidate)
containing the locations in criterions of the
first element for each subset size. For I = 0, 1,
..., nsize −1, element
numbers index_criterions[I], index_criterions[I] + 1, ..., index_criterions[I + 1] − 1 of criterions correspond
to the (I +
1)-st subset size. Argument criterions is the
address of a pointer to the internally allocated array of length max (index_criterions
[nsize] − 1 ,
n_candidate)
containing in its first index_criterions
[nsize] − 1 elements
the criterion values for each subset considered, in increasing subset size
order.
IMSLS_CRITERIONS_USER, int
index_criterions[],
float criterions[]
(Output)
Storage for arrays index_criterions and
criterions is
provided by the user. An upper bound on the length of criterions is
max(max_n_good_saved × nsize,
n_candidate).
See IMSLS_CRITERIONS.
IMSLS_INDEPENDENT_VARIABLES, int
**index_variables, int **independent_variables
(Output)
Argument index_variables is the
address of a pointer to the internally allocated array of length nsize +
1 (where nsize is equal to max_subset_size if
optional argument IMSLS_R_SQUARED is
specified; otherwise, nsize is equal to n_candidate)
containing the locations in independent_variables
of the first element for each subset size. For I = 0, 1,
..., nsize − 1, element
numbers index_variables[I], index_variables[I] + 1, ...,
index_variables[I + 1] − 1 of independent_variables
correspond to the (I+1)-st subset size.
Argument independent_variables
is the address of a pointer to the internally allocated array of length index_variables
[nsize] − 1
containing the variable numbers for each subset considered and in the same order
as in criterions.
IMSLS_INDEPENDENT_VARIABLES_USER, int index_variables[],
int independent_variables[]
(Output)
Storage for arrays index_variables and
independent_variables
is provided by the user. An upper bound for the length of independent_variables
is as follows:
where nsize is equal to max_subset_size.
See IMSLS_INDEPENDENT_VARIABLES.
IMSLS_COEF_STATISTICS, int
**index_coefficients,
float **coefficients
(Output)
Argument index_coefficients is
the address of a pointer to the internally allocated array of length
ntbest + 1 containing the locations in coefficients or the
first row for each of the best regressions. Here, ntbest is the total
number of best regression found and is equal to max_subset_size × max_n_best if IMSLS_R_SQUARED is
specified, equal to max_n_best if either
IMSLS_MALLOWS_CP
or IMSLS_ADJ_R_SQUARED is
specified, and equal to max_n_best × n_candidate,
otherwise. For I = 0, 1,
..., ntbest − 1, rows index_coefficients[I], index_coefficients[I] + 1, ...,
index_coefficients[I + 1] – 1
of coefficients
correspond to the (I + 1)-st regression.
Argument coefficients is the
address of a pointer to the internally allocated array of size (index_coefficients
[ntbest] − 1) ×
5 containing statistics relating to the regression coefficients of the best
models. Each row corresponds to a coefficient for a particular regression. The
regressions are in order of increasing subset size. Within each subset size, the
regressions are ordered so that the better regressions appear first. The
statistic in the columns are as follows (inferences are conditional on the
selected model):
|
Column |
Description |
|
0 |
variable number |
|
1 |
coefficient estimate. |
|
2 |
estimated standard error of the estimate |
|
3 |
t-statistic for the test that the coefficient is 0 |
|
4 |
t-statistic for the test that the coefficient is 0 |
IMSLS_COEF_STATISTICS_USER, int
index_coefficients[],
float coefficients[]
(Output)
Storage for arrays index_coefficients and
coefficients is
provided by the user. See IMSLS_COEF_STATISTICS.
IMSLS_INPUT_COV, int n_observations, float cov[]
(Input)
Argument n_observations is the
number of observations associated with array cov. Argument cov is an (n_candidate + 1) by
(n_candidate +
1) array containing a variance-covariance or sum of squares and crossproducts
matrix, in which the last column must correspond to the dependent variable.
Array cov can be
computed using imsls_f_covariances.
Arguments x and
y, and optional
arguments frequencies and weights are not
accessed when this option is specified. Normally, imsls_f_regression_selection
computes cov
from the input data matrices x and y. However, there may
be cases when the user will wish to calculate the covariance matrix and
manipulate it before calling imsls_f_regression_selection.
See the description section below for a discussion of such cases.
Description
Function imsls_f_regression_selection finds the best subset regressions for a regression problem with n_candidate independent variables. Typically, the intercept is forced into all models and is not a candidate variable. In this case, a sum of squares and crossproducts matrix for the independent and dependent variables corrected for the mean is computed internally. There may be cases when it is convenient for the user to calculate the matrix; see the description of optional argument IMSLS_INPUT_COV.
“Best” is defined, on option, by one of the following three criteria:
• R2 (in percent)
• 
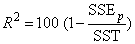
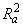(adjusted R2 in percent)
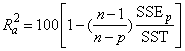
Note that maximizing the criterion is equivalent to minimizing the residual mean square:
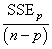
• Mallows’ Cp statistic
Here, n is equal to the sum of the frequencies (or
n_rows
if IMSLS_FREQUENCIES
is not specified) and SST is the total sum of squares.
SSEp is
the error sum of squares in a model containing p regression parameters
including β0 (or
p − 1 of the
n_candidate
candidate variables). Variable
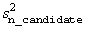
is the error mean square from the model with all n_candidate variables in the model. Hocking (1972) and Draper and Smith (1981, pp. 296−302) discuss these criteria.
Function imsls_f_regression_selection is based on the algorithm of Furnival and Wilson (1974). This algorithm finds max_n_good_saved candidate regressions for each possible subset size. These regressions are used to identify a set of best regressions. In large problems, many regressions are not computed. They may be rejected without computation based on results for other subsets; this yields an efficient technique for considering all possible regressions.
There are cases when the user may want to input the variance-covariance matrix rather than allow the function imsls_f_regression_selection to calculate it. This can be accomplished using optional argument IMSLS_INPUT_COV. Three situations in which the user may want to do this are as follows:
1. The intercept is not in the model. A raw (uncorrected) sum of squares and crossproducts matrix for the independent and dependent variables is required. Argument n_observations must be set to 1 greater than the number of observations. Form ATA, where A = [A, Y], to compute the raw sum of squares and crossproducts matrix.
2. An intercept is a candidate variable. A raw (uncorrected) sum of squares and crossproducts matrix for the constant regressor (= 1.0), independent, and dependent variables is required for cov. In this case, cov contains one additional row and column corresponding to the constant regressor. This row/column contains the sum of squares and crossproducts of the constant regressor with the independent and dependent variables. The remaining elements in cov are the same as in the previous case. Argument n_observations must be set to 1 greater than the number of observations.
3. There are m variables to be forced into the models. A sum of squares and crossproducts matrix adjusted for the m variables is required (calculated by regressing the candidate variables on the variables to be forced into the model). Argument n_observations must be set to m less than the number of observations.
Programming Notes
Function imsls_f_regression_selection can save considerable CPU time over explicitly computing all possible regressions. However, the function has some limitations that can cause unexpected results for users who are unaware of the limitations of the software.
1. For n_candidate + 1 > −log2 (ɛ), where ɛ is imsls_f_machine(4) and (imsls_d_machine(4) for double precision; see Chapter 15 , “Ultilities), some results can be incorrect. This limitation arises because the possible models indicated (the model numbers 1, 2, ..., 2n_candidate) are stored as floating-point values; for sufficiently large n_candidate, the model numbers cannot be stored exactly. On many computers, this means imsls_f_regression_selection (for n_candidate > 24) and imsls_d_regression_selection (for n_candidate > 49) can produce incorrect results.
2. Function imsls_f_regression_selection eliminates some subsets of candidate variables by obtaining lower bounds on the error sum of squares from fitting larger models. First, the full model containing all n_candidate is fit sequentially using a forward stepwise procedure in which one variable enters the model at a time, and criterion values and model numbers for all the candidate variables that can enter at each step are stored. If linearly dependent variables are removed from the full model, error IMSLS_VARIABLES_DELETED is issued. If this error is issued, some submodels that contain variables removed from the full model because of linear dependency can be overlooked if they have not already been identified during the initial forward stepwise procedure. If error IMSLS_VARIABLES_DELETED is issued and you want the variables that were removed from the full model to be considered in smaller models, you can rerun the program with a set of linearly independent variables.
Examples
Example 1
This example uses a data set from Draper and Smith (1981, pp. 629−630). Function imsls_f_regression_selection is invoked to find the best regression for each subset size using the R2 criterion. By default, the function prints the results.
#include <imsls.h>
#define N_OBSERVATIONS 13
#define N_CANDIDATE 4
int main()
{
float x[N_OBSERVATIONS][N_CANDIDATE] =
{7., 26., 6., 60.,
1., 29., 15., 52.,
11., 56., 8., 20.,
11., 31., 8., 47.,
7., 52., 6., 33.,
11., 55., 9., 22.,
3., 71., 17., 6.,
1., 31., 22., 44.,
2., 54., 18., 22.,
21., 47., 4., 26.,
1., 40., 23., 34.,
11., 66., 9., 12.,
10., 68., 8., 12.};
float y[N_OBSERVATIONS] = {78.5, 74.3, 104.3, 87.6, 95.9,
109.2, 102.7, 72.5, 93.1, 115.9, 83.8, 113.3, 109.4};
imsls_f_regression_selection(N_OBSERVATIONS, N_CANDIDATE, x, y, 0);
}
Output
Regressions with 1 variable(s) (R-squared)
Criterion Variables
67.5 4
66.6 2
53.4 1
28.6 3
Regressions with 2 variable(s) (R-squared)
Criterion Variables
97.9 1 2
97.2 1 4
93.5 3 4
68 2 4
54.8 1 3
Regressions with 3 variable(s) (R-squared)
Criterion Variables
98.2 1 2 4
98.2 1 2 3
98.1 1 3 4
97.3 2 3 4
Regressions with 4 variable(s) (R-squared)
Criterion Variables
98.2 1 2 3 4
Best Regression with 1 variable(s) (R-squared)
Variable Coefficient Standard Error t-statistic p-value
4 -0.7382 0.1546 -4.775 0.0006
Best Regression with 2 variable(s) (R-squared)
Variable Coefficient Standard Error t-statistic p-value
1 1.468 0.1213 12.10 0.0000
2 0.662 0.0459 14.44 0.0000
Best Regression with 3 variable(s) (R-squared)
Variable Coefficient Standard Error t-statistic p-value
1 1.452 0.1170 12.41 0.0000
2 0.416 0.1856 2.24 0.0517
4 -0.237 0.1733 -1.36 0.2054
Best Regression with 4 variable(s) (R-squared)
Variable Coefficient Standard Error t-statistic p-value
1 1.551 0.7448 2.083 0.0708
2 0.510 0.7238 0.705 0.5009
3 0.102 0.7547 0.135 0.8959
4 -0.144 0.7091 -0.203 0.8441
Example 2
This example uses the same data set as the first example, but Mallow’s Cp statistic is used as the criterion rather than R2. Note that when Mallow’s Cp statistic (or adjusted R2) is specified, the variable max_n_best indicates the total number of “best” regressions (rather than indicating the number of best regressions per subset size, as in the case of the R2 criterion). In this example, the three best regressions are found to be (1, 2), (1, 2, 4), and (1, 2, 3).
#include <imsls.h>
#define N_OBSERVATIONS 13
#define N_CANDIDATE 4
int main()
{
float x[N_OBSERVATIONS][N_CANDIDATE] =
{7., 26., 6., 60.,
1., 29., 15., 52.,
11., 56., 8., 20.,
11., 31., 8., 47.,
7., 52., 6., 33.,
11., 55., 9., 22.,
3., 71., 17., 6.,
1., 31., 22., 44.,
2., 54., 18., 22.,
21., 47., 4., 26.,
1., 40., 23., 34.,
11., 66., 9., 12.,
10., 68., 8., 12.};
float y[N_OBSERVATIONS] = {78.5, 74.3, 104.3, 87.6, 95.9,
109.2, 102.7, 72.5, 93.1, 115.9, 83.8, 113.3, 109.4};
int max_n_best = 3;
imsls_f_regression_selection(N_OBSERVATIONS, N_CANDIDATE,
(float *) x, y,
IMSLS_MALLOWS_CP,
IMSLS_MAX_N_BEST, max_n_best,
0);
}
Output
1
Regressions with 1 variable(s) (Mallows CP)
Criterion Variables
139 4
142 2
203 1
315 3
Regressions with 2 variable(s) (Mallows CP)
Criterion Variables
2.68 1 2
5.5 1 4
22.4 3 4
138 2 4
198 1 3
Regressions with 3 variable(s) (Mallows CP)
Criterion Variables
3.02 1 2 4
3.04 1 2 3
3.5 1 3 4
7.34 2 3 4
Regressions with 4 variable(s) (Mallows CP)
Criterion Variables
5 1 2 3 4
1
Best Regression with 2 variable(s) (Mallows CP)
Variable Coefficient Standard Error t-statistic p-value
1 1.468 0.1213 12.10 0.0000
2 0.662 0.0459 14.44 0.0000
Best Regression with 3 variable(s) (Mallows CP)
Variable Coefficient Standard Error t-statistic p-value
1 1.452 0.1170 12.41 0.0000
2 0.416 0.1856 2.24 0.0517
4 -0.237 0.1733 -1.36 0.2054
2nd Best Regression with 3 variable(s) (Mallows CP)
Variable Coefficient Standard Error t-statistic p-value
1 1.696 0.2046 8.29 0.0000
2 0.657 0.0442 14.85 0.0000
3 0.250 0.1847 1.35 0.2089
Warning Errors
IMSLS_VARIABLES_DELETED At least one variable is deleted from the full model because the variance-covariance matrix “cov” is singular.
Fatal Errors
IMSLS_NO_VARIABLES No variables can enter any model.
