Computes a cubic spline interpolant, specifying various endpoint conditions. The default interpolant satisfies the “not-a-knot” condition.

The type Imsl_d_ppoly function is imsl_d_cub_spline_interp_e_cnd.

A pointer to the structure that represents the cubic spline interpolant. If an interpolant cannot be computed, then NULL is returned. To release this space, use imsl_free.

IMSL_RIGHT, int iright, float right (Input)
Set the value for the first or second derivative of the interpolant at the right endpoint. If iright = i, then the interpolant s satisfies

The function imsl_f_cub_spline_interp_e_cnd computes a C2 cubic spline interpolant to a set of data points (xi, fi) for i = 0, …, ndata − 1 = n. The breakpoints of the spline are the abscissas. We emphasize here that for all the univariate interpolation functions, the abscissas need not be sorted. Endpoint conditions are to be selected by the user. The user may specify “not-a-knot” or first derivative or second derivative at each endpoint, or C2 periodicity may be requested (see de Boor 1978, Chapter 4). If no defaults are selected, then the “not-a-knot” spline interpolant is computed. If the IMSL_PERIODIC keyword is selected, then all other keywords are ignored; and a C2 periodic interpolant is computed. In this case, if the fdata values at the left and right endpoints are not the same, then a warning message is issued; and we set the right value equal to the left. If IMSL_LEFT or IMSL_RIGHT are selected (in the absence of IMSL_PERIODIC), then the user has the ability to select the values of the first or second derivative at either endpoint. The default case (when the keyword is not used) is the “not-a-knot” condition on that endpoint. Thus, when no optional arguments are chosen, this function produces the “not-a-knot” interpolant.

If the data (including the endpoint conditions) arise from the values of a smooth (say C4) function f, i.e. fi = f(xi), then the error will behave in a predictable fashion. Let ξ be the breakpoint vector for the above spline interpolant. Then, the maximum absolute error satisfies

where

For more details, see de Boor (1978, Chapters 4 and 5).

The return value for this function is a pointer to the structure Imsl_f_ppoly. The calling program must receive this in a pointer Imsl_f_ppoly *ppoly. This structure contains all the information to determine the spline (stored as a piecewise polynomial) that is computed by this function. For example, the following code sequence evaluates this spline at x and returns the value in y

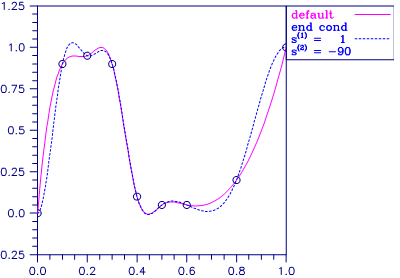
The difference between the default (“not-a-knot”) spline and the interpolating cubic spline, which has first derivative set to 1 at the left end and the second derivative set to −90 at the right end, is illustrated in the following figure.

In this example, a cubic spline interpolant to a function f is computed. The values of this spline are then compared with the exact function values. Since we are using the default settings, the interpolant is determined by the “not-a-knot” condition (see de Boor 1978).

In this example, a cubic spline interpolant to a function f is computed. The value of the derivative at the left endpoint and the value of the second derivative at the right endpoint are specified. The values of this spline are then compared with the exact function values.

This example computes the natural cubic spline interpolant to a function f by forcing the second derivative of the interpolant to be zero at both endpoints. As in the previous example, the exact function values are computed with the values of the spline.

This example computes the cubic spline interpolant to a functions, and imposes the periodic end conditions s(a) = s(b), s'(a) = s'(b), and s"(a) = s"(b), where a is the leftmost abscissa and b is the rightmost abscissa.