chi_squared_cdf
Evaluates the chi‑squared cumulative distribution function (CDF).
Synopsis
#include <imsl.h>
float imsl_f_chi_squared_cdf (float chi_squared, float df)
The type double function is imsl_d_chi_squared_cdf.
Required Arguments
float chi_squared (Input)
Argument for which the chi‑squared distribution function is to be evaluated.
float df (Input)
Number of degrees of freedom of the chi‑squared distribution. Argument df must be greater than 0.
Return Value
The probability p that a chi‑squared random variable takes a value less than or equal to chi_squared.
Description
Function imsl_f_chi_squared_cdf evaluates the distribution function, F(x,ν), of a chi‑squared random variable x = chi_squared with ν = df degrees of freedom, where:
and Γ (⋅) is the gamma function. The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.
For
ν>
νmax = 1.e7,
imsl_f_chi_squared_cdf uses the Wilson-Hilferty approximation (Abramowitz and Stegun [A&S] 1964, Equation 26.4.17) for
p in terms of the normal CDF, which is evaluated using function
imsl_f_normal_cdf.
For ν≤ νmax, imsl_f_chi_squared_cdf uses series expansions to evaluate p: for x < ν, imsl_f_chi_squared_cdf calculates p using A&S series 6.5.29, and for x≥ν, imsl_f_chi_squared_cdf calculates p using the continued fraction expansion of the incomplete gamma function given in A&S equation 6.5.31.
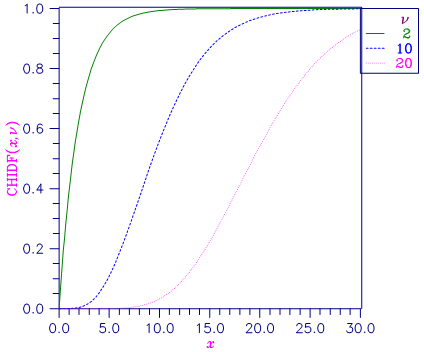
Figure 9.21 — Plot of Fx (x, df)
Example
Suppose X is a chi‑squared random variable with two degrees of freedom. In this example, we find the probability that X is less than 0.15 and the probability that X is greater than 3.0.
#include <imsl.h>
#include <stdio.h>
int main()
{
float chi_squared = 0.15, df = 2.0, p;
p = imsl_f_chi_squared_cdf(chi_squared, df);
printf("The probability that chi-squared"
" with %1.0f df is less than %4.2f is %5.4f\n",
df, chi_squared, p);
chi_squared = 3.0;
p = 1.0 - imsl_f_chi_squared_cdf(chi_squared, df);
printf("The probability that chi-squared"
" with %1.0f df is greater than %3.1f is %5.4f\n",
df, chi_squared, p);
}
Output
The probability that chi-squared with 2 df is less than 0.15 is 0.0723
The probability that chi-squared with 2 df is greater than 3.0 is 0.2231
Informational Errors
IMSL_ARG_LESS_THAN_ZERO | Since “chi_squared” = #is less than zero, the distribution function is zero at “chi_squared.” |
Alert Errors
IMSL_NORMAL_UNDERFLOW | Using the normal distribution for large degrees of freedom, underflow would have occurred. |