complementary_chi_squared_cdf

Evaluates the complement of the chi-squared cumulative distribution function (CDF).

Synopsis

#include <imsls.h>

float imsls_f_complementary_chi_squared_cdf (float chi_squared, float df)

The type double function is imsls_d_complementary_chi_squared_cdf.

Required Arguments

float chi_squared (Input)
Argument for which the complementary chi-squared distribution function is to be evaluated.

float df (Input)
Number of degrees of freedom of the complementary chi-squared distribution. df must be greater than 0.

Return Value

The probability p that a chi-squared random variable takes a value greater than chi_squared.

Description

Function imsls_f_complementary_chi_squared_cdf evaluates the complement of the CDF, , of a chi-squared random variable x = chi_squared with ν = df degrees of freedom, where,

 

is the chi-squared CDF and Γ (⋅) is the gamma function. The value of the complementary chi‑squared CDF at the point x is the probability that the random variable takes a value greater than x.

For ν > vmax = 1.e7, imsls_f_complementary_chi_squared_cdf uses the Wilson-Hilferty approximation (Abramowitz and Stegun [A&S] 1964, Equation 26.4.17) for p in terms of the normal CDF, which is evaluated using function imsls_f_normal_cdf.

For v ≤ vmax, imsls_f_complementary_chi_squared_cdf uses series expansions to evaluate p: for x < ν, imsls_f_complementary_chi_squared_cdf calculates p using A&S series 6.5.29, and for x ≥ ν, imsls_f_complementary_chi_squared_cdf calculates p using the continued fraction expansion of the incomplete gamma function given in A&S equation 6.5.31.

Function imsls_f_complementary_chi_squared_cdf provides higher right tail accuracy for the complementary chi-squared distribution than does function 1 ‑ imsls_f_chi_squared_cdf.

 

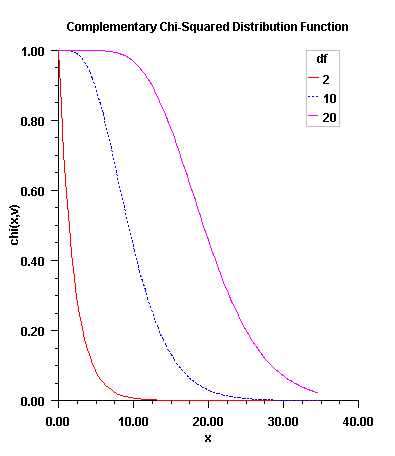
Figure 1,  Plot of Fx (x, df)

Example

In this example, we find the probability that X, a chi-squared random variable, is less than 0.15 and the probability that X is greater than 3.0.

 

#include <imsls.h>

#include <stdio.h>

 

int main()

{

    float chi_squared = 0.15, df = 2.0, p;

 

    p = imsls_f_chi_squared_cdf(chi_squared, df);

    printf("The probability that chi-squared\n");

    printf(" with df = %1.0f is less than %4.2f is %6.4f\n",

        df, chi_squared, p);

 

    chi_squared = 3.0;

    p = imsls_f_complementary_chi_squared_cdf(chi_squared, df);

    printf("The probability that chi-squared\n");

    printf(" with df = %1.0f is greater than %4.2f is %6.4f\n",

        df, chi_squared, p);

}

Output

 

The probability that chi-squared

with df = 2 is less than 0.15 is 0.0723

The probability that chi-squared

with df = 2 is greater than 3.00 is 0.2231

Informational Errors

IMSLS_COMP_CHISQ_ZERO

Since “chi_squared” = # is less than zero, the distribution function is one at “chi_squared”.