mlff_network_trainer
Trains a multilayered feedforward neural network.
Synopsis
#include <imsls.h>
float *imsls_f_mlff_network_trainer (Imsls_f_NN_Network *network, int n_patterns, int n_nominal, int n_continuous, int nominal[], float continuous[], float output[], ..., 0)
The type double function is imsls_d_mlff_network_trainer.
Required Arguments
Imsls_f_NN_Network *network (Input/Output)
Pointer to a structure of type Imsls_f_NN_Network containing the feedforward network. See imsls_f_mlff_network. On return, the weights and bias values are updated.
int n_patterns (Input)
Number of network training patterns.
int n_nominal (Input)
Number of nominal attributes. n_nominal + n_continuous must equal n_inputs, where n_inputs is the number of input attributes in the network. n_inputs = network->n_inputs. For more details, see imsls_f_mlff_network.
int n_continuous (Input)
Number of continuous attributes. n_nominal + n_continuous must equal n_inputs, where n_inputs is the number of input attributes in the network. n_inputs = network->n_inputs. For more details, see imsls_f_mlff_network.
int nominal[] (Input)
Array of size n_patterns by n_nominal containing values for the nominal input attributes. The i-th row contains the nominal input attributes for the i-th training pattern.
float continuous[] (Input)
Array of size n_patterns by n_continuous containing values for the continuous input attributes. The i-th row contains the continuous input attributes for the i-th training pattern.
float output[] (Input)
Array of size n_patterns by n_outputs containing the output training patterns, where n_outputs is the number of output perceptrons in the network.
Return Value
An array of length 5 containing the summary statistics from the network training, organized as follows:
|
Element |
Training Statistics |
|
0 |
Error sum of squares at the optimum. |
|
1 |
Total number of Stage I iterations. |
|
2 |
Smallest error sum of squares after Stage I training. |
|
3 |
Total number of Stage II iterations. |
|
4 |
Smallest error sum of squares after Stage II training. |
This space can be released by using the imsls_free function.
If training is unsuccessful, NULL is returned.
Synopsis with Optional Arguments
#include <imsls.h>
float *imsls_f_mlff_network_trainer (Imsls_f_NN_Network *network, int n_patterns, int n_nominal, int n_continuous, float nominal[], int continuous[], float output[],
IMSLS_STAGE_I, int n_epochs, int epoch_size,
IMSLS_NO_STAGE_II,
IMSLS_MAX_STEP, float max_step,
IMSLS_MAX_ITN, int max_itn,
IMSLS_MAX_FCN, int max_fcn,
IMSLS_REL_FCN_TOL, float rfcn_tol,
IMSLS_GRAD_TOL, float grad_tol,
IMSLS_TOLERANCE, float tolerance,
IMSLS_WEIGHT_INITIALIZATION_METHOD, int method,
IMSLS_PRINT,
IMSLS_RESIDUAL, float **residuals,
IMSLS_RESIDUAL_USER, float residuals[],
IMSLS_GRADIENT, float **gradients,
IMSLS_GRADIENT_USER, float gradients[],
IMSLS_FORECASTS, float **forecasts,
IMSLS_FORECASTS_USER, float forecasts[],
IMSLS_RETURN_USER, float z[],
0)
Optional Arguments
IMSLS_STAGE_I, int n_epochs, int epoch_size (Input)
Argument n_epochs is the number epochs used for Stage I training and argument epoch_size is the number of patterns used during each epoch. If epoch training is not needed, set epoch_size = n_patterns and n_epochs = 1. Stage I is implemented using Quasi-Newton optimization and steepest ascent with gradients estimated using the backward propagation method.
Default: n_epochs=15, epoch_size = n_patterns.
IMSLS_NO_STAGE_II, (Input)
Specifies no Stage II training is performed. Stage II is implemented using Quasi-Newton optimization with numerical gradients.
Default: Stage II training is performed.
IMSLS_MAX_STEP, float max_step (Input)
Maximum allowable step size in the optimizer.
Default: max_step = 1000.
IMSLS_MAX_ITN, int max_itn (Input)
Maximum number of iterations in the optimizer, per epoch.
Default: max_itn = 1000.
IMSLS_MAX_FCN, int max_fcn (Input)
Maximum number of function evaluations in the optimizer, per epoch.
Default: max_fcn = 400.
IMSLS_REL_FCN_TOL, float rfcn_tol (Input)
Relative function tolerance in the optimizer.
Default: rfcn_tol = max (10-10, ɛ2/3), where ɛ is the machine precision, max (10-20, ɛ2/3) is used in double precision.
IMSLS_GRAD_TOL, float grad_tol (Input)
Scaled gradient tolerance in the optimizer.
Default: grad_tol = ɛ1/2, where ɛ is the machine precision, ɛ1/3 is used in double precision.
IMSLS_TOLERANCE, float tolerance (Input)
Absolute accuracy tolerance for the sum of squared errors in the optimizer.
Default: tolerance = 0.1.
IMSLS_WEIGHT_INITIALIZATION_METHOD, int method[] (Input)
The method to use for initializing network weights prior to network training. One of the following four values is accepted:
|
method |
Algorithm |
|
IMSLS_EQUAL |
Equal weights. |
|
IMSLS_RANDOM |
Random weights. |
|
IMSLS_PRINCIPAL_COMPONENTS |
Principal Component Weights. |
|
IMSLS_NN_NETWORK |
No initialization method will be performed. Weights in imsls_f_NN_Network structure network will be used instead. |
See imsls_f_mlff_initialize_weights for a detailed description of the initialization methods.
Default: method = IMSLS_RANDOM.
IMSLS_PRINT, (Input)
Intermediate results are printed during network training.
Default: No printing is performed.
IMSLS_RESIDUAL, float **residuals (Output)
The address of a pointer to the internally allocated array of size n_patterns by n_outputs containing the residuals for each observation in the training data, where n_outputs is the number of output perceptrons in the network.
n_outputs = network->n_outputs.
IMSLS_RESIDUAL_USER, float residuals[] (Output)
Storage for array residuals provided by user. See IMSLS_RESIDUAL.
IMSLS_GRADIENT, float **gradients (Output)
The address of a pointer to the internally allocated array of size n_links + n_nodes-n_inputs to store the gradients for each weight found at the optimum training stage, where n_links = network->n_links, n_nodes = network->n_nodes, and
IMSLS_GRADIENT_USER, float gradients[] (Output)
Storage for array gradients provided by user. See IMSLS_GRADIENT.
IMSLS_FORECASTS, float **forecasts (Output)
The address of a pointer to the internally allocated array of size n_patterns by n_outputs, where n_outputs is the number of output perceptrons in the network.
n_outputs = network->n_outputs. The values of the i-th row are the forecasts for the outputs for the i-th training pattern.
IMSLS_FORECASTS_USER, float forecasts[] (Output)
Storage for array forecasts is provided by user. See IMSLS_FORECASTS.
IMSLS_RETURN_USER, float z[] (Output)
User-supplied array of length 5. Upon completion, z contains the return array of training statistics. See Return Value for details.
Description
Function imsls_f_mlff_network_trainer trains a multilayered feedforward neural network returning the forecasts for the training data, their residuals, the optimum weights and the gradients associated with those weights. Linkages among perceptrons allow for skipped layers, including linkages between inputs and perceptrons. The linkages and activation function for each perceptron, including output perceptrons, can be individually configured. For more details, see optional arguments IMSLS_LINK_ALL, IMSLS_LINK_LAYER, and IMSLS_LINK_NODE in imsls_f_mlff_network.
Training Data
Neural network training patterns consist of the following three types of data:
| 1. | nominal input attributes |
| 2. | continuous input attributes |
| 3. | continuous output |
The first data type contains the encoding of any nominal input attributes. If binary encoding is used, this encoding consists of creating columns of zeros and ones for each class value associated with every nominal attribute. If only one attribute is used for input, then the number of columns is equal to the number of classes for that attribute. If more columns appear in the data, then each nominal attribute is associated with several columns, one for each of its classes.
Each column consists of zeros, if that classification is not associated with this case, otherwise, one if that classification is associated. Consider an example with one nominal variable and two classes: male and female (male, male, female, male, female). With binary encoding, the following matrix is sent to the training engine to represent this data:

Continuous input and output data are passed to the training engine using two double precision arrays: continuous and output. The number of rows in each of these matrices is n_patterns. The number of columns in continuous and output, corresponds to the number of input and output variables, respectively.
Network Configuration
The network configuration consists of the following:
| • | the number of inputs and outputs, |
| • | the number of hidden layers, |
| • | a description of the number of perceptrons in each layer, |
| • | and a description of the linkages among the perceptrons. |
This description is passed into imsls_f_mlff_network_trainer using the structure Imsls_f_NN_Network. See imsls_f_mlff_network.
Training Efficiency
The training efficiency determines the time it takes to train the network. This is controlled by several factors. One of the most important factors is the initial weights used by the optimization algorithm. These are taken from the initial values provided in the structure Imsls_f_NN_Network, network‑>links[i].weight. Equally important are the scaling and filtering applied to the training data.
In most cases, all variables, particularly output variables, should be scaled to fall within a narrow range, such as [0, 1]. If variables are unscaled and have widely varied ranges, then numerical overflow conditions can terminate network training before an optimum solution is calculated.
Output
Output from imsls_f_mlff_network_trainer consists of scaled values for the network outputs, a corresponding forecast array for these outputs, a weights array for the trained network, and the training statistics. The Imsls_f_NN_Network structure is updated with the weights and bias values and can be used as input to imsls_f_mlff_network_forecast.
The trained network can be saved and retrieved using imsls_f_mlff_network_write and imsls_f_mlff_network_read.
Example
This example trains a two-layer network using 100 training patterns from one nominal and one continuous input attribute. The nominal attribute has three classifications which are encoded using binary encoding. This results in three binary network input columns. The continuous input attribute is scaled to fall in the interval [0,1].
The network training targets were generated using the relationship:
Y = 10*X1 + 20*X2 + 30*X3 + 20*X4,
where X1, X2, X3 are the three binary columns, corresponding to the categories 1‑3 of the nominal attribute, and X4 is the scaled continuous attribute.
The structure of the network consists of four input nodes and two layers, with three perceptrons in the hidden layer and one in the output layer. The following figure illustrates this structure:
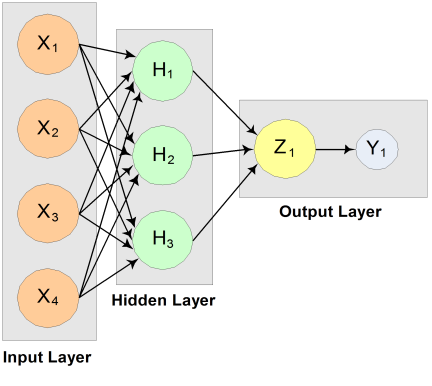
Figure 1, A 2-layer, Feedforward Network with 4 Inputs and 1 Output
There are a total of 15 weights and 4 bias weights in this network. The activation functions are all linear.
Since the target output is a linear function of the input attributes, linear activation functions guarantee that the network forecasts will exactly match their targets. Of course, the same result could have been obtained using multiple regression. Printing is turned on to show progress during the training session.
#include <imsls.h>
#include <stdio.h>
int main()
{
/* A 2D matrix of values for the nominal training attribute. In this
* example, the single nominal attribute has 3 categories that are
* encoded using binary encoding for input into the network.
*
* {1,0,0} = category 1
* {0,1,0} = category 2
* {0,0,1} = category 3
*/
int nominal[300] =
{
1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,
1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,
1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,
1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,
0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,
0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,
0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,
0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,
0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,
0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,
0,0,1,0,0,1,0,0,1,0,0,1,0,0,1
};
/* A matrix of values for the continuous training attribute */
float continuous[100] = {
4.007054658,7.10028447,4.740350984,5.714553211,6.205437459,
2.598930065,8.65089967,5.705787357,2.513348184,2.723795955,
4.1829356,1.93280416,0.332941608,6.745567628,5.593588463,
7.273544478,3.162117939,4.205381208,0.16414745,2.883418275,
0.629342241,1.082223406,8.180324708,8.004894314,7.856215418,
7.797143157,8.350033996,3.778254431,6.964837082,6.13938006,
0.48610387,5.686627923,8.146173848,5.879852653,4.587492779,
0.714028533,7.56324211,8.406012623,4.225261454,6.369220241,
4.432772218,9.52166984,7.935791508,4.557155333,7.976015058,
4.913538616,1.473658514,2.592338905,1.386872932,7.046051685,
1.432128376,1.153580985,5.6561491,3.31163251,4.648324851,
5.042514515,0.657054195,7.958308093,7.557870384,7.901990083,
5.2363088,6.95582150,8.362167045,4.875903563,1.729229471,
4.380370223,8.527875685,2.489198107,3.711472959,4.17692681,
5.844828801,4.825754155,5.642267843,5.339937786,4.440813223,
1.615143829,7.542969339,8.100542684,0.98625265,4.744819569,
8.926039258,8.813441887,7.749383991,6.551841576,8.637046998,
4.560281415,1.386055087,0.778869034,3.883379045,2.364501589,
9.648737525,1.21754765,3.908879368,4.253313879,9.31189696,
3.811953836,5.78471629,3.414486452,9.345413015,1.024053777
};
/* A 2D matrix containing the training outputs for this network.
In this case there is an exact linear relationship between these
outputs and the inputs: output = 10*X1 +20*X2 + 30*X3 +2*X4,
where X1-X3 are the categorical variables and X4 is the continuous
attribute variable. Output is unscaled.
*/
float output[100];
Imsls_f_NN_Network *network;
float *stats;
int n_patterns= 100, n_nominal=3, n_continuous=1;
int i,j,k, wIdx;
float *residuals, *forecasts;
float bias, coef1, coef2, coef3, coef4;
int hidActFcn[3] = {IMSLS_LINEAR,IMSLS_LINEAR,IMSLS_LINEAR};
/* Scale continuous attribute into the interval [0, 1]
and generate outputs */
for(i=0; i < 100; i++)
{
continuous[i] = continuous[i]/10.0;
output[i] = (10 * nominal[i*3]) + (20 * nominal[i*3+1]) +
(30 * nominal[i*3+2]) + (20 * continuous[i]);
}
/* Create network */
network = imsls_f_mlff_network_init(4,1);
imsls_f_mlff_network(network, IMSLS_CREATE_HIDDEN_LAYER, 3,
IMSLS_ACTIVATION_FCN, 1, &hidActFcn,
IMSLS_LINK_ALL, 0);
/* Set initial weights */
for (j=network->n_inputs; j < network->n_nodes ; j++)
{
for (k=0; k < network->nodes[j].n_inLinks; k++)
{
wIdx = network->nodes[j].inLinks[k];
/* set specific layer weights */
if (network->nodes[j].layer_id == 1) {
network->links[wIdx].weight = 0.25;
} else if (network->nodes[j].layer_id == 2) {
network->links[wIdx].weight = 0.33;
}
}
}
/* Initialize seed for consisten results */
imsls_random_seed_set(12345);
stats = imsls_f_mlff_network_trainer(network, n_patterns,
n_nominal, n_continuous, nominal, continuous, output,
IMSLS_STAGE_I, 10, 100,
IMSLS_MAX_FCN, 1000,
IMSLS_REL_FCN_TOL, 1.0e-20,
IMSLS_GRAD_TOL, 1.0e-20,
IMSLS_MAX_STEP, 5.0,
IMSLS_TOLERANCE, 1.0e-5,
IMSLS_PRINT,
IMSLS_RESIDUAL, &residuals,
IMSLS_FORECASTS, &forecasts,
0);
printf("Predictions for Last Ten Observations: \n");
for(i=90; i < 100; i++){
printf("observation[%d] %f Prediction %f Residual %f \n", i,
output[i], forecasts[i], residuals[i]);
}
/* hidden layer nodes bias value * link weight */
bias = network->nodes[network->n_nodes-4].bias *
network->links[12].weight +
network->nodes[network->n_nodes-3].bias *
network->links[13].weight +
network->nodes[network->n_nodes-2].bias *
network->links[14].weight;
/* the bias of the output node */
bias += network->nodes[network->n_nodes-1].bias;
coef1 = network->links[0].weight * network->links[12].weight;
coef1 += network->links[1].weight * network->links[13].weight;
coef1 += network->links[2].weight * network->links[14].weight;
coef2 = network->links[3].weight * network->links[12].weight;
coef2 += network->links[4].weight * network->links[13].weight;
coef2 += network->links[5].weight * network->links[14].weight;
coef3 = network->links[6].weight * network->links[12].weight;
coef3 += network->links[7].weight * network->links[13].weight;
coef3 += network->links[8].weight * network->links[14].weight;
coef4 = network->links[9].weight * network->links[12].weight;
coef4 += network->links[10].weight * network->links[13].weight;
coef4 += network->links[11].weight * network->links[14].weight;
coef1 += bias;
coef2 += bias;
coef3 += bias;
printf("Bias: %f \n", bias);
printf("X1: %f \n", coef1);
printf("X2: %f \n", coef2);
printf("X3: %f \n", coef3);
printf("X4: %f \n", coef4);
imsls_f_mlff_network_free(network);
}
Output
TRAINING PARAMETERS:
Stage II Opt. = 1
n_epochs = 10
epoch_size = 100
max_itn = 1000
max_fcn = 1000
max_step = 5.000000
rfcn_tol = 1e-020
grad_tol = 1e-020
tolerance = 0.000010
STAGE I TRAINING STARTING
Stage I: Epoch 1 - Epoch Error SS = 3870.44 (Iterations=7)
Stage I: Epoch 2 - Epoch Error SS = 7.41238e-011 (Iterations=74)
Stage I Training Converged at Epoch = 2
STAGE I FINAL ERROR SS = 0.000000
OPTIMUM WEIGHTS AFTER STAGE I TRAINING:
weight[0] = 2.29881 weight[1] = 4.67622 weight[2] = 5.82167
weight[3] = 2.01955 weight[4] = 3.02815 weight[5] = 5.61873
weight[6] = 9.46591 weight[7] = 7.44722 weight[8] = 1.82561
weight[9] = 6.08981 weight[10] = 11.1714 weight[11] = 5.30152
weight[12] = 2.15733 weight[13] = 2.26835 weight[14] = -0.23573
weight[15] = -3.4723 weight[16] = 0.100865 weight[17] = 2.71152
weight[18] = 6.50345
STAGE I TRAINING CONVERGED
STAGE I ERROR SS = 0.000000
GRADIENT AT THE OPTIMUM WEIGHTS
g[0] = 0.000014 weight[0] = 2.298808
g[1] = 0.000045 weight[1] = 4.676218
g[2] = -0.000012 weight[2] = 5.821669
g[3] = 0.000026 weight[3] = 2.019547
g[4] = 0.000015 weight[4] = 3.028149
g[5] = 0.000048 weight[5] = 5.618728
g[6] = -0.000013 weight[6] = 9.465913
g[7] = 0.000027 weight[7] = 7.447217
g[8] = -0.000002 weight[8] = 1.825613
g[9] = -0.000005 weight[9] = 6.089811
g[10] = 0.000001 weight[10] = 11.171391
g[11] = -0.000003 weight[11] = 5.301523
g[12] = 0.000028 weight[12] = 2.157330
g[13] = 0.000176 weight[13] = 2.268351
g[14] = 0.000199 weight[14] = -0.235730
g[15] = 0.000047 weight[15] = -3.472301
g[16] = 0.000050 weight[16] = 0.100865
g[17] = -0.000005 weight[17] = 2.711518
g[18] = 0.000022 weight[18] = 6.503448
Training Completed
Predictions for Last Ten Observations:
observation[90] 49.297478 Prediction 49.297474 Residual -0.000004
observation[91] 32.435097 Prediction 32.435093 Residual -0.000004
observation[92] 37.817757 Prediction 37.817760 Residual 0.000004
observation[93] 38.506630 Prediction 38.506630 Residual 0.000000
observation[94] 48.623795 Prediction 48.623795 Residual 0.000000
observation[95] 37.623909 Prediction 37.623909 Residual 0.000000
observation[96] 41.569431 Prediction 41.569431 Residual 0.000000
observation[97] 36.828972 Prediction 36.828972 Residual 0.000000
observation[98] 48.690826 Prediction 48.690830 Residual 0.000004
observation[99] 32.048107 Prediction 32.048107 Residual 0.000000
Bias: -1.397840
X1: 10.000000
X2: 20.000000
X3: 30.000000
X4: 20.000000
