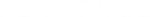CWPQ

This function evaluates the Weierstrass’ ℘ function in the equianharmonic case for complex argument with unit period parallelogram.

Function Return Value

CWPQ — Complex function value. (Output)

Required Arguments

Z — Complex argument for which the function value is desired. (Input)

FORTRAN 90 Interface

Generic: CWPQ (Z)

Specific: The specific interface names are C_CWPQ and Z_CWPQ.

FORTRAN 77 Interface

Complex:     CWPQ (Z)

Double complex:   The double complex name is ZWPQ.

Description

The Weierstrass’ ℘ function, ℘(z) = ℘(z ∣ ω, ωʹ), is an elliptic function of order two with periods 2 ω and 2 ωʹ and a double pole at z = 0. CWPQ(Z) computes ℘(z ∣ ω, ωʹ) with

 

The input argument is first reduced to the fundamental parallelogram of all z satisfying

 

Then, a rational approximation is used.

All arguments are valid with the exception of the lattice points

 

which are the poles of CWPQ. If the argument is a lattice point, then b = AMACH(2), the largest floating‑point number, is returned. If the argument has modulus greater than 10ɛ−1, then NaN (not a number) is returned. Here, ɛ = AMACH(4) is the machine precision.

Function CWPQ is based on code by Eckhardt (1980). Also, see Eckhardt (1977).

Example

In this example, ℘(0.25 + 0.14437567i) is computed and printed.

 

USE CWPQ_INT

USE UMACH_INT

 

IMPLICIT NONE

! Declare variables

INTEGER NOUT

COMPLEX VALUE, Z

! Compute

Z = (0.25, 0.14437567)

VALUE = CWPQ(Z)

! Print the results

CALL UMACH (2, NOUT)

WRITE (NOUT,99999) Z, VALUE

99999 FORMAT (' CWPQ(', F6.3, ',', F6.3, ') = (', &

F7.3, ',', F7.3, ')')

END

Output

 

CWPQ( 0.250, 0.144) = ( 5.895,-10.216)