TDF

This function evaluates the Student’s t cumulative distribution function.

Function Return Value

TDF — Function value, the probability that a Student’s t random variable takes a value less than or equal to the input T. (Output)

Required Arguments

T — Argument for which the Student’s t distribution function is to be evaluated. (Input)

DF — Degrees of freedom. (Input)
DF must be greater than or equal to 1.0.

Optional Arguments

COMPLEMENT — Logical. If .TRUE., the complement of the Student’s t cumulative distribution function is evaluated. If .FALSE., the Student’s t cumulative distribution function is evaluated. (Input)
See the Description section for further details on the use of COMPLEMENT.
Default: COMPLEMENT = .FALSE..

FORTRAN 90 Interface

Generic: TDF (T, DF [, …])

Specific: The specific interface names are S_TDF and D_TDF.

FORTRAN 77 Interface

Single: TDF (T, DF)

Double: The double precision name is DTDF.

Description

Function TDF evaluates the cumulative distribution function of a Student’s t random variable with DF degrees of freedom. If the square of T is greater than or equal to DF, the relationship of a t to an F random variable (and subsequently, to a beta random variable) is exploited, and routine BETDF is used. Otherwise, the method described by Hill (1970) is used. Let ν = DF. If ν is not an integer, if ν is greater than 19, or if ν is greater than 200, a Cornish‑Fisher expansion is used to evaluate the distribution function. If ν is less than 20 and ABS(T) is less than 2.0, a trigonometric series (see Abramowitz and Stegun 1964, equations 26.7.3 and 26.7.4, with some rearrangement) is used. For the remaining cases, a series given by Hill (1970) that converges well for large values of T is used.

If COMPLEMENT = .TRUE., the value of TDF at the point x is 1 ‑ p, where 1 ‑ p is the probability that the random variable takes a value greater than x. In those situations where the desired end result is 1– p, the user can achieve greater accuracy in the right tail region by using the result returned by TDF with the optional argument COMPLEMENT set to .TRUE. rather than by using 1 ‑ p where p is the result returned by TDF with COMPLEMENT set to .FALSE..

 

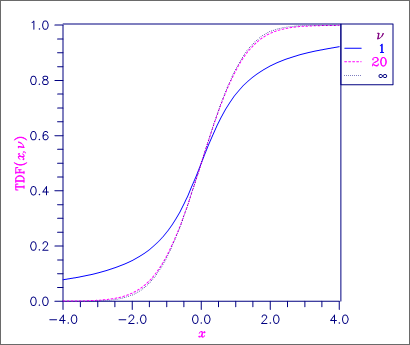
Figure 1,  Student’s t Distribution Function

Example

In this example, we find the probability that a t random variable with 6 degrees of freedom is greater in absolute value than 2.447. We use the fact that t is symmetric about 0.

 

USE TDF_INT

USE UMACH_INT

IMPLICIT NONE

INTEGER NOUT

REAL DF, P, T

!

CALL UMACH (2, NOUT)

T = 2.447

DF = 6.0

P = 2.0*TDF(-T,DF)

WRITE (NOUT,99999) P

99999 FORMAT (' The probability that a t(6) variate is greater ', &

'than 2.447 in', /, ' absolute value is ', F6.4)

END

Output

 

The probability that a t(6) variate is greater than 2.447 in absolute value is 0.0500