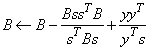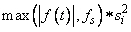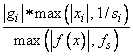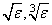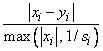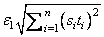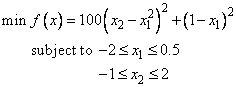Minimizes a function of N variables subject to bounds on the variables using a quasi-Newton method and a finite-difference gradient.

Required Arguments

FCN — User-supplied subroutine to evaluate the function to be minimized. The usage is CALL FCN (N, X, F), where

N – Length of X.   (Input)

X – Vector of length N at which point the function is evaluated.   (Input)
X should not be changed by FCN.

F – The computed function value at the point X.   (Output)

FCN must be declared EXTERNAL in the calling program.

IBTYPE — Scalar indicating the types of bounds on variables.   (Input)

IBTYPE                  Action

0                              User will supply all the bounds.

1                              All variables are nonnegative.

2                              All variables are nonpositive.

3                              User supplies only the bounds on 1st variable, all other variables will have                     the same bounds.

XLB — Vector of length N containing the lower bounds on variables.   (Input, if IBTYPE = 0; output, if IBTYPE = 1 or 2; input/output, if IBTYPE = 3)

XUB — Vector of length N containing the upper bounds on variables.   (Input, if IBTYPE = 0; output, if IBTYPE = 1 or 2; input/output, if IBTYPE = 3)

X — Vector of length N containing the computed solution.   (Output)

Optional Arguments

N — Dimension of the problem.   (Input)
Default: N = size (X,1).

XGUESS — Vector of length N containing an initial guess of the computed solution.   (Input)
Default: XGUESS = 0.0.

XSCALE — Vector of length N containing the diagonal scaling matrix for the variables.   (Input)
XSCALE is used mainly in scaling the gradient and the distance between two points. In the absence of other information, set all entries to 1.0.
Default: XSCALE = 1.0.

FSCALE — Scalar containing the function scaling.   (Input)
FSCALE is used mainly in scaling the gradient. In the absence of other information, set FSCALE to 1.0.
Default: FSCALE = 1.0.

IPARAM — Parameter vector of length 7.   (Input/Output)
Set IPARAM(1) to zero for default values of IPARAM and RPARAM. See Comment 4.
Default: IPARAM = 0.

RPARAM — Parameter vector of length 7.   (Input/Output)
See Comment 4.

FVALUE — Scalar containing the value of the function at the computed solution.   (Output)

FORTRAN 90 Interface

Generic:          CALL BCONF (FCN, IBTYPE, XLB, XUB, X [,…])

Specific:         The specific interface names are S_BCONF and D_BCONF.

FORTRAN 77 Interface

Single:            CALL BCONF (FCN, N, XGUESS, IBTYPE, XLB, XUB, XSCALE, FSCALE, IPARAM, RPARAM, X, FVALUE)

Double:          The double precision name is DBCONF.

Description

The routine BCONF uses a quasi-Newton method and an active set strategy to solve minimization problems subject to simple bounds on the variables. The problem is stated as follows:

subject to l ≤ x ≤ u

From a given starting point xc, an active set IA, which contains the indices of the variables at their bounds, is built. A variable is called a “free variable” if it is not in the active set. The routine then computes the search direction for the free variables according to the formula

d = -B-1 gc

where B is a positive definite approximation of the Hessian and gc is the gradient evaluated at xc; both are computed with respect to the free variables. The search direction for the variables in IA is set to zero. A line search is used to find a new point xn ,

xn = xc + λd,     λ ∈ (0, 1]

such that

f (xn) ≤ f (xc) + αgT d,        α ∈ (0, 0.5)

Finally, the optimality conditions

||g(xi)|| ≤ ɛ, li < xi< ui

g(xi) < 0,  xi = ui

g(xi) > 0, xi = li

are checked, where ɛ is a gradient tolerance. When optimality is not achieved, B is updated according to the BFGS formula:

where s = xn - xc and y = gn - gc. Another search direction is then computed to begin the next iteration.

The active set is changed only when a free variable hits its bounds during an iteration or the optimality condition is met for the free variables but not for all variables in IA, the active set. In the latter case, a variable that violates the optimality condition will be dropped out of IA. For more details on the quasi-Newton method and line search, see Dennis and Schnabel (1983). For more detailed information on active set strategy, see Gill and Murray (1976).

Since a finite-difference method is used to estimate the gradient for some single precision calculations, an inaccurate estimate of the gradient may cause the algorithm to terminate at a noncritical point. In such cases, high precision arithmetic is recommended. Also, whenever the exact gradient can be easily provided, routine BCONG should be used instead.

Comments

1.         Workspace may be explicitly provided, if desired, by use of B2ONF/DB2ONF. The reference is:

CALL B2ONF (FCN, N, XGUESS, IBTYPE, XLB, XUB, XSCALE, FSCALE, IPARAM, RPARAM, X, FVALUE, WK, IWK)

The additional arguments are as follows:

WK — Real work vector of length N * (2 * N + 8). WK contains the following information on output: The second N locations contain the last step taken. The third N locations contain the last Newton step. The fourth N locations contain an estimate of the gradient at the solution. The final N2 locations contain a BFGS approximation to the Hessian at the solution.  Only the lower triangular portion of the matrix is stored in WK. The values returned in the upper triangle should be ignored.

IWK — Work vector of length N stored in column order.

2.         Informational errors

Type   Code

3           1                  Both the actual and predicted relative reductions in the function are less than or equal to the relative function convergence tolerance.

4           2                  The iterates appear to be converging to a noncritical point.

4           3                  Maximum number of iterations exceeded.

4           4                  Maximum number of function evaluations exceeded.

4           5                  Maximum number of gradient evaluations exceeded.

4           6                  Five consecutive steps have been taken with the maximum step length.

2           7                  Scaled step tolerance satisfied; the current point may be an approximate local solution, or the algorithm is making very slow progress and is not near a solution, or STEPTL is too big.

3           8                  The last global step failed to locate a lower point than the current X value.

3.         The first stopping criterion for BCONF occurs when the norm of the gradient is less than the given gradient tolerance (RPARAM(1)). The second stopping criterion for BCONF occurs when the scaled distance between the last two steps is less than the step tolerance (RPARAM(2)).

4.         If the default parameters are desired for BCONF, then set IPARAM(1) to zero and call the routine BCONF. Otherwise, if any nondefault parameters are desired for IPARAM or RPARAM, then the following steps should be taken before calling BCONF:

CALL U4INF (IPARAM, RPARAM)

Set nondefault values for desired IPARAM, RPARAM elements.

Note that the call to U4INF will set IPARAM and RPARAM to their default values so only nondefault values need to be set above.

The following is a list of the parameters and the default values:

IPARAM — Integer vector of length 7.

IPARAM(1) = Initialization flag.

IPARAM(2) = Number of good digits in the function.

Default: Machine dependent.

IPARAM(3) = Maximum number of iterations.

Default: 100.

IPARAM(4) = Maximum number of function evaluations.

Default: 400.

IPARAM(5) = Maximum number of gradient evaluations.

Default: 400.

IPARAM(6) = Hessian initialization parameter.
If IPARAM(6) = 0, the Hessian is initialized to the identity matrix; otherwise,
it is initialized to a diagonal matrix containing

            on the diagonal where t = XGUESS, fs = FSCALE, and s = XSCALE.

Default: 0.

IPARAM(7) = Maximum number of Hessian evaluations.

Default: Not used in BCONF.

RPARAM — Real vector of length 7.

RPARAM(1) = Scaled gradient tolerance.
The i-th component of the scaled gradient at x is calculated as

            where g = ∇f(x), s = XSCALE, and fs = FSCALE.

Default:

            in double where ɛ is the machine precision.

RPARAM(2) = Scaled step tolerance. (STEPTL)
The i-th component of the scaled step between two points x and y is computed as

where s = XSCALE.

Default: ɛ2/3 where ɛ is the machine precision.

RPARAM(3) = Relative function tolerance.

Default: Not used in BCONF.

RPARAM(4) = Absolute function tolerance.

Default: Not used in BCONF.

RPARAM(5) = False convergence tolerance.

Default: Not used in BCONF.

RPARAM(6) = Maximum allowable step size.

Default: 1000 max(ɛ1, ɛ2) where

ɛ2 = || s ||2, s = XSCALE, and t = XGUESS.

RPARAM(7) = Size of initial trust region radius.

Default: based on the initial scaled Cauchy step.

If double precision is required, then DU4INF is called and RPARAM is declared double precision.

5.         Users wishing to override the default print/stop attributes associated with error messages issued by this routine are referred to “Error Handling” in the Introduction.

Example

The problem

is solved with an initial guess (-1.2, 1.0) and default values for parameters.

 

      USE BCONF_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

      INTEGER    N

      PARAMETER  (N=2)

!

      INTEGER    IPARAM(7), ITP, L, NOUT

      REAL       F, FSCALE, RPARAM(7), X(N), XGUESS(N), &

                XLB(N), XSCALE(N), XUB(N)

      EXTERNAL   ROSBRK

!

      DATA XGUESS/-1.2E0, 1.0E0/

      DATA XLB/-2.0E0, -1.0E0/, XUB/0.5E0, 2.0E0/

!                                 All the bounds are provided

      ITP = 0

!                                 Default parameters are used

      IPARAM(1) = 0

!                                 Minimize Rosenbrock function using

!                                 initial guesses of -1.2 and 1.0

      CALL BCONF (ROSBRK, ITP, XLB, XUB, X, XGUESS=XGUESS,  &

                 iparam=iparam, FVALUE=F)

!                                 Print results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) X, F, (IPARAM(L),L=3,5)

!

99999 FORMAT ('  The solution is ', 6X, 2F8.3, //, '  The function ', &

            'value is ', F8.3, //, '  The number of iterations is ', &

            10X, I3, /, '  The number of function evaluations is ', &

            I3, /, '  The number of gradient evaluations is ', I3)

!

      END

!

      SUBROUTINE ROSBRK (N, X, F)

      INTEGER    N

      REAL       X(N), F

!

      F = 1.0E2*(X(2)-X(1)*X(1))**2 + (1.0E0-X(1))**2

!

      RETURN

      END

Output

 

The solution is          0.500   0.250

The function value is    0.250

The number of iterations is            24
The number of function evaluations is  34
The number of gradient evaluations is  26

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260