This function evaluates the integral of a tensor-product spline on a rectangular domain, given its tensor-product B-spline representation.

Function Return Value

BS2IG — Integral of the spline over the rectangle (A, B) by (C, D).
(Output)

Required Arguments

A — Lower limit of the X-variable.   (Input)

B — Upper limit of the X-variable.   (Input)

C — Lower limit of the Y-variable.   (Input)

D — Upper limit of the Y-variable.   (Input)

KXORD — Order of the spline in the X-direction.   (Input)

KYORD — Order of the spline in the Y-direction.   (Input)

XKNOT — Array of length NXCOEF + KXORD containing the knot sequence in the X-direction.   (Input)
XKNOT must be nondecreasing.

YKNOT — Array of length NYCOEF + KYORD containing the knot sequence in the Y-direction.   (Input)
YKNOT must be nondecreasing.

BSCOEF — Array of length NXCOEF * NYCOEF containing the tensor-product B-spline coefficients.   (Input)
BSCOEF is treated internally as a matrix of size NXCOEF by NYCOEF.

Optional Arguments

NXCOEF — Number of B-spline coefficients in the X-direction.   (Input)
Default: NXCOEF = size (XKNOT,1) – KXORD.

NYCOEF — Number of B-spline coefficients in the Y-direction.   (Input)
Default: NYCOEF = size (YKNOT,1) – KYORD.

FORTRAN 90 Interface

Generic:          BS2IG (A, B, C, D, KXORD, KYORD, XKNOT, YKNOT, BSCOEF [,…])

Specific:         The specific interface names are S_BS2IG and D_BS2IG.

FORTRAN 77 Interface

Single:     BS2IG (A, B, C, D, KXORD, KYORD, XKNOT, YKNOT, NXCOEF, NYCOEF, BSCOEF)

Double:          The double precision function name is DBS2IG.

Description

The function BS2IG computes the integral of a tensor-product two-dimensional spline given its
B-spline representation. Specifically, given the knot sequence tx = XKNOT, ty = YKNOT, the order
kx = KXORD, ky = KYORD, the coefficients β = BSCOEF, the number of coefficients nx = NXCOEF,
ny = NYCOEF and a rectangle [a, b] by [c, d], BS2IG returns the value

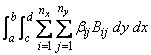
where

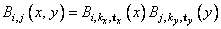
This routine uses the identity (22) on page 151 of de Boor (1978). It assumes (for all knot sequences) that the first and last k knots are stacked, that is,t1 = … = tk and tn + 1 = … = tn + k, where k is the order of the spline in the x or y direction.

Comments

1.         Workspace may be explicitly provided, if desired, by use of B22IG/DB22IG. The reference is:

CALL B22IG(A, B, C, D, KXORD, KYORD, XKNOT, YKNOT, NXCOEF, NYCOEF, BSCOEF, WK)

The additional argument is:

WK — Work array of length 4 * (MAX(KXORD, KYORD) + 1) + NYCOEF.

2.         Informational errors

Type   Code

3           1                  The lower limit of the X-integration is less than XKNOT(KXORD).

3           2                  The upper limit of the X-integration is greater than XKNOT(NXCOEF + 1).

3           3                  The lower limit of the Y-integration is less than YKNOT(KYORD).

3           4                  The upper limit of the Y-integration is greater than YKNOT(NYCOEF + 1).

4           13                Multiplicity of the knots cannot exceed the order of the spline.

4           14                The knots must be nondecreasing.

Example

We integrate the two-dimensional tensor-product quartic (kx = 5) by linear (ky = 2) spline that interpolates x3 + xy at the points {(i/10, j/5) : i = −10, …, 10 and j = 0, …, 5} over the rectangle
[0, 1] × [.5, 1]. The exact answer is 5/16.

 

      USE BS2IG_INT

      USE BSNAK_INT

      USE BS2IN_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                                  SPECIFICATIONS FOR PARAMETERS

      INTEGER    KXORD, KYORD, LDF, NXDATA, NXKNOT, NYDATA, NYKNOT

      PARAMETER  (KXORD=5, KYORD=2, NXDATA=21, NYDATA=6, LDF=NXDATA,&

                 NXKNOT=NXDATA+KXORD, NYKNOT=NYDATA+KYORD)

!

      INTEGER    I, J, NOUT, NXCOEF, NYCOEF

      REAL       A, B, BSCOEF(NXDATA,NYDATA), C , D, F,&

                 FDATA(LDF,NYDATA), FI, FLOAT, VAL, X, XDATA(NXDATA),&

                 XKNOT(NXKNOT), Y, YDATA(NYDATA), YKNOT(NYKNOT)

      INTRINSIC  FLOAT

!                                  Define function and integral

      F(X,Y)      = X*X*X + X*Y

      FI(A,B,C ,D) = .25*((B**4-A**4)*(D-C )+(B*B-A*A)*(D*D-C *C ))

!                                  Set up interpolation points

      DO 10  I=1, NXDATA

         XDATA(I) = FLOAT(I-11)/10.0

   10 CONTINUE

!                                  Generate knot sequence

      CALL BSNAK (NXDATA, XDATA, KXORD, XKNOT)

!                                  Set up interpolation points

      DO 20  I=1, NYDATA

         YDATA(I) = FLOAT(I-1)/5.0

   20 CONTINUE

!                                  Generate knot sequence

      CALL BSNAK (NYDATA, YDATA, KYORD, YKNOT)

!                                  Generate FDATA

      DO 40  I=1, NYDATA

         DO 30  J=1, NXDATA

            FDATA(J,I) = F(XDATA(J),YDATA(I))

   30  CONTINUE

   40 CONTINUE

!                                  Interpolate

      CALL BS2IN (XDATA, YDATA, FDATA, KXORD,&

                  KYORD, XKNOT, YKNOT, BSCOEF)

!                                  Integrate over rectangle

!                                  [0.0,1.0] x [0.0,0.5]

      NXCOEF = NXDATA

      NYCOEF = NYDATA

      A      = 0.0

      B      = 1.0

      C       = 0.5

      D      = 1.0

      VAL    = BS2IG(A,B,C ,D,KXORD,KYORD,XKNOT,YKNOT,BSCOEF)

!                                  Get output unit number

      CALL UMACH (2, NOUT)

!                                  Print results

      WRITE (NOUT,99999) VAL, FI(A,B,C ,D), FI(A,B,C ,D) - VAL

99999 FORMAT (' Computed Integral = ', F10.5, /, ' Exact Integral    '&

             , '= ', F10.5, /, ' Error             '&

             , '= ', F10.6, /)

      END

Output

 

Computed Integral =    0.31250
Exact Integral    =    0.31250
Error             =   0.000000

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260