This function evaluates the integral of a spline, given its B-spline representation.
Function Return Value
BSITG — Value of the integral of the spline from A to B. (Output)
Required Arguments
A — Lower limit of integration. (Input)
B — Upper limit of integration. (Input)
KORDER — Order of the spline. (Input)
XKNOT — Array of
length KORDER +
NCOEF containing
the knot sequence. (Input)
XKNOT must be
nondecreasing.
NCOEF — Number of B-spline coefficients. (Input)
BSCOEF — Array of length NCOEF containing the B-spline coefficients. (Input)
FORTRAN 90 Interface
Generic: BSITG (A, B, KORDER, XKNOT, NCOEF, BSCOEF)
Specific: The specific interface names are S_BSITG and D_BSITG.
FORTRAN 77 Interface
Single: BSITG (A, B, KORDER, XKNOT, NCOEF, BSCOEF)
Double: The double precision function name is DBSITG.
Description
The function BSITG
computes the integral of a spline given its B-spline representation.
Specifically, given the knot sequence t = XKNOT,
the order k = KORDER,
the coefficients
a = BSCOEF
, n = NCOEF
and an interval [a, b], BSITG
returns the value
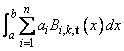
This routine uses the identity (22) on page 151 of de Boor (1978), and it assumes that t1 = … = tk and tn + 1= … = tn + k.
Comments
1. Workspace may be explicitly provided, if desired, by use of B2ITG/DB2ITG. The reference is:
CALL B2ITG(A, B, KORDER, XKNOT, NCOEF, BSCOEF, TCOEF, AJ, DL, DR)
The additional arguments are as follows:
TCOEF — Work array of length KORDER + 1.
AJ — Work array of length KORDER + 1.
DL — Work array of length KORDER + 1.
DR — Work array of length KORDER + 1.
2. Informational errors
Type Code
3 7 The upper and lower endpoints of integration are equal.
3 8 The lower limit of integration is less than XKNOT(KORDER).
3 9 The upper limit of integration is greater than XKNOT(NCOEF + 1).
4 4 Multiplicity of the knots cannot exceed the order of the spline.
4 5 The knots must be nondecreasing.
Example
We integrate the quartic (k = 5) spline that interpolates x3 at the points {i/10 : i = −10, …, 10} over the interval [0, 1]. The exact answer is 1/4 since the interpolant reproduces cubic polynomials.
USE BSITG_INT
USE BSNAK_INT
USE BSINT_INT
USE UMACH_INT
IMPLICIT NONE
INTEGER KORDER, NDATA, NKNOT
PARAMETER (KORDER=5, NDATA=21, NKNOT=NDATA+KORDER)
!
INTEGER I, NCOEF, NOUT
REAL A, B, BSCOEF(NDATA), ERROR, EXACT, F,&
FDATA(NDATA), FI, FLOAT, VAL, X, XDATA(NDATA),&
XKNOT(NKNOT)
INTRINSIC FLOAT
! Define function and integral
F(X) = X*X*X
FI(X) = X**4/4.0
! Set up interpolation points
DO 10 I=1, NDATA
XDATA(I) = FLOAT(I-11)/10.0
FDATA(I) = F(XDATA(I))
10 CONTINUE
! Generate knot sequence
CALL BSNAK (NDATA, XDATA, KORDER, XKNOT)
! Interpolate
CALL BSINT (NDATA, XDATA, FDATA, KORDER, XKNOT, BSCOEF)
! Get output unit number
CALL UMACH (2, NOUT)
!
NCOEF = NDATA
A = 0.0
B = 1.0
! Integrate from A to B
VAL = BSITG(A,B,KORDER,XKNOT,NCOEF,BSCOEF)
EXACT = FI(B) - FI(A)
ERROR = EXACT - VAL
! Print results
WRITE (NOUT,99999) A, B, VAL, EXACT, ERROR
99999 FORMAT (' On the closed interval (', F3.1, ',', F3.1,&
') we have :', /, 1X, 'Computed Integral = ', F10.5, /,&
1X, 'Exact Integral = ', F10.5, /, 1X, 'Error '&
, ' = ', F10.6, /, /)
END
Output
On the closed interval (0.0,1.0) we have :
Computed
Integral = 0.25000
Exact Integral
= 0.25000
Error
=
0.000000
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |