Computes the not-a-knot spline knot sequence.
Required Arguments
NDATA Number of data points. (Input)
XDATA Array of length NDATA containing the location of the data points. (Input)
KORDER Order of the spline. (Input)
XKNOT Array of length NDATA + KORDER containing the knot sequence. (Output)
FORTRAN 90 Interface
Generic: CALL BSNAK (NDATA, XDATA, KORDER, XKNOT)
Specific: The specific interface names are S_BSNAK and D_BSNAK.
FORTRAN 77 Interface
Single: CALL BSNAK (NDATA, XDATA, KORDER, XKNOT)
Double: The double precision name is DBSNAK.
Description
Given the data points x = XDATA , the order of the spline k = KORDER, and the number N = NDATA of elements in XDATA, the subroutine BSNAK returns in t = XKNOT a knot sequence that is appropriate for interpolation of data on x by splines of order k. The vector t contains the knot sequence in its first N + k positions. If k is even and we assume that the entries in the input vector x are increasing, then t is returned as
ti = x1 for i = 1, , k
ti = xi - k/2 for i = k + 1, , N
ti = xN + ɛ for i = N + 1, , N + k
where ɛ is a small positive constant. There is some discussion concerning this selection of knots in de Boor (1978, page 211). If k is odd, then t is returned as
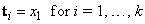
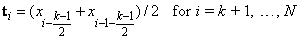
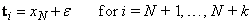
It is not necessary to sort the values in x since this is done in the routine BSNAK.
Comments
1. Workspace may be explicitly provided, if desired, by use of B2NAK/DB2NAK. The reference is:
CALL B2NAK (NDATA, XDATA, KORDER, XKNOT, XSRT, IWK)
The additional arguments are as follows:
XSRT Work array of length NDATA to hold the sorted XDATA values. If XDATA is not needed, XSRT may be the same as XDATA.
IWK Work array of length NDATA to hold the permutation of XDATA.
2. Informational error
Type Code
4 4 The XDATA values must be distinct.
3. The first knot is at the left endpoint and the last knot is slightly beyond the last endpoint. Both endpoints have multiplicity KORDER.
4. Interior knots have multiplicity one.
Example
In this example, we compute (for k = 3, , 8) six spline interpolants sk to F(x) = sin(10x3) on the interval [0,1]. The routine BSNAK is used to generate the knot sequences for sk and then BSINT is called to obtain the interpolant. We evaluate the absolute error
|sk − F|
at 100 equally spaced points and print the maximum error for each k.
USE IMSL_LIBRARIES
IMPLICIT NONE
INTEGER KMAX, KMIN, NDATA
PARAMETER (KMAX=8, KMIN=3, NDATA=20)
!
INTEGER I, K, KORDER, NOUT
REAL ABS, AMAX1, BSCOEF(NDATA), DIF, DIFMAX, F,&
FDATA(NDATA), FLOAT, FT, SIN, ST, T, X, XDATA(NDATA),&
XKNOT(KMAX+NDATA), XT
INTRINSIC ABS, AMAX1, FLOAT, SIN
! Define function and tau function
F(X) = SIN(10.0*X*X*X)
T(X) = 1.0 - X*X
! Set up data
DO 10 I=1, NDATA
XT = FLOAT(I-1)/FLOAT(NDATA-1)
XDATA(I) = T(XT)
FDATA(I) = F(XDATA(I))
10 CONTINUE
! Get output unit number
CALL UMACH (2, NOUT)
! Write heading
WRITE (NOUT,99999)
! Loop over different orders
DO 30 K=KMIN, KMAX
KORDER = K
! Generate knots
CALL BSNAK (NDATA, XDATA, KORDER, XKNOT)
! Interpolate
CALL BSINT (NDATA, XDATA, FDATA, KORDER, XKNOT, BSCOEF)
DIFMAX = 0.0
DO 20 I=1, 100
XT = FLOAT(I-1)/99.0
! Evaluate spline
ST = BSVAL(XT,KORDER,XKNOT,NDATA,BSCOEF)
FT = F(XT)
DIF = ABS(FT-ST)
! Compute maximum difference
DIFMAX = AMAX1(DIF,DIFMAX)
20 CONTINUE
! Print maximum difference
WRITE (NOUT,99998) KORDER, DIFMAX
30 CONTINUE
!
99998 FORMAT (' ', I3, 5X, F9.4)
99999 FORMAT (' KORDER', 5X, 'Maximum difference', /)
END
Output
KORDER Maximum
difference
3
0.0080
4
0.0026
5
0.0004
6
0.0008
7
0.0010
8 0.0004
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |