Solves a linear programming problem.
NOTE: DENSE_LP is available in double precision only.
Required Arguments
A — M by NVAR matrix containing the coefficients of the M constraints. (Input)
BL — Vector of length M containing the lower limit of the general constraints; if there is no lower limit on the I-th constraint, then BL(I) is not referenced. (Input)
BU — Vector of length M containing the upper limit of the general constraints; if there is no upper limit on the I-th constraint, then BU(I) is not referenced; if there are no range constraints, BL and BU can share the same storage locations. (Input)
C — Vector of length NVAR containing the coefficients of the objective function. (Input)
IRTYPE — Vector
of length M
indicating the types of general constraints in the matrix A. (Input)
Let R(I) = A(I, 1) * XSOL(1) + … + A(I, NVAR) * XSOL(NVAR). Then, the value
of IRTYPE(I) signifies the
following:
|
Irtype[I] |
I-th Constraint |
|
0 |
BL(I) = R(I) = BU(I) |
|
1 |
R(I) ≤ BU(I) |
|
2 |
R(I) ≥ BL(I) |
|
3 |
BL(I) ≤ R(I) ≤ BU(I) |
|
4 |
Ignore this constraint |
OBJ — Value of the objective function. (Output)
XSOL — Vector of length NVAR containing the primal solution.(Output)
DSOL — Vector of length M containing the dual solution. (Output)
Optional Arguments
M — Number of
constraints. (Input)
Default: M = size (A,1).
NVAR — Number of
variables. (Input)
Default: NVAR = size
(A,2).
LDA — Leading
dimension of A
exactly as specified in the dimension statement of the calling
program. (Input)
LDA must be at least
M.
Default:
LDA = size
(A,1).
XLB — Vector of
length NVAR
containing the lower bound on the variables; if there is no lower bound on a
variable, then 1.0D30 should be set as the lower bound.
(Input)
Default: XLB = 0.0D0.
XUB — Vector of
length NVAR
containing the upper bound on the variables; if there is no upper bound on a
variable, then -1.0D30 should be set as
the upper bound. (Input)
Default: No upperbound enforced.
ITREF — The type
if iterative refinement used. (Input)
|
ITREF |
Refinement |
|
0 |
No refinement |
|
1 |
Iterative refinement |
|
2 |
Use extended refinement. Iterate until no more progress. |
Default: ITREF = 0.
ITERS — Number of iterations. (Output)
IERR — Status flag indicating which warning conditions were set upon completion. (Output)
|
Status | |
|
≥0 |
Solution found. IERR = 0 indicates there are no warning conditions. If the solution was found with warning conditions IERR is incremented by the number given below. |
|
1 |
1 is added to the value returned if there are multiple solutions giving essentially the same minimum. |
|
2 |
2 is added to the value returned if there were some constraints discarded because they were too linearly dependent on other active constraints. |
|
4 |
4 is added to the value returned if the constraints were not satisfied. L1 minimization was applied to all (including bounds on simple variables) but the equalities, to approximate violated non-equalities as well as possible. If a feasible solution is possible then refinement may help |
|
8 |
8 is added to the value returned if the algorithm appears to be cycling. Using refinement may help. |
FORTRAN 90 Interface
Generic: CALL DENSE_LP (A, BL, BU, C, IRTYPE, OBJ, XSOL, DSOL [,…])
Specific: The specific interface name is D_DENSE_LP. This subroutine is available in double precision only.
Description
The routine DENSE_LP solves the linear programming problem
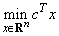
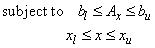
where c is the objective coefficient vector, A is the coefficient matrix, and the vectors bl, bu, xl and xu are the lower and upper bounds on the constraints and the variables, respectively.
DENSE_LP uses an active set strategy.
Refer to the following paper for further information: Krogh, Fred, T. (2005), An Algorithm for Linear Programming, http://mathalacarte.com/fkrogh/pub/lp.pdf ,Tujunga, CA.
Comments
1. Informational errors
Type Code
1 1 Multiple solutions giving essentially the same solution exist.
3 1 Some constraints were discarded because they were too linearly dependent on other active constraints.
3 2 All constraints are not satisfied.
3 3 The algorithm appears to be cycling.
4 1 The problem appears vacuous.
4 2 The problem is unbounded.
4 3 An acceptable pivot could not be found.
4 4 The constraint bounds are inconsistent.
4 5 The variable bounds are inconsistent.
Example 1
The linear programming problem in the standard form

is solved.
USE UMACH_INT
USE WRRRN_INT
USE DENSE_LP_INT
IMPLICIT NONE
INTEGER NOUT, M, NVAR
PARAMETER (M=4, NVAR=6)
DOUBLE PRECISION A(M, NVAR), B(M), C(NVAR), XSOL(NVAR), &
DSOL(M), BL(M), BU(M), OBJ
INTEGER IRTYPE(M)
DATA A/1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, -1, &
0, 0, 0, 0, 1, 0, 0, 0, 0, 1/
DATA B/1.5, 0.5, 1.0, 1.0/
DATA C/-1.0, -3.0, 0.0, 0.0, 0.0, 0.0/
DATA BL/1.5, 0.5, 1.0, 1.0/
DATA BU/M*-1.D30/
DATA IRTYPE/M*0/
CALL UMACH(2, NOUT)
! Solve the LP problem
CALL DENSE_LP (A, BL, BU, C, IRTYPE, OBJ, XSOL, DSOL)
WRITE(NOUT, 99999) OBJ
CALL WRRRN('Solution', XSOL, 1, NVAR, 1)
99999 FORMAT (' Objective', F9.4)
END
Output
Objective -3.5000
Solution
1 2 3 4 5 6
0.500 1.000 0.000 1.000 0.500 0.000
Additional Examples
Example 2
This example demonstrates how READ_MPS can be used together with DENSE_LP to solve a linear programming problem defined in an MPS file. The MPS file used in this example is an uncompressed version of the file ‘afiro', available from http://www.netlib.org/lp/data/.
USE UMACH_INT
USE WRRRN_INT
USE READ_MPS_INT
USE DENSE_LP_INT
IMPLICIT NONE
REAL(KIND(1D0)) OBJ
REAL(KIND(1D0)), ALLOCATABLE :: XSOL(:)
REAL(KIND(1D0)), ALLOCATABLE :: DSOL(:)
REAL(KIND(1D0)), ALLOCATABLE :: A(:,:)
INTEGER, ALLOCATABLE :: IRTYPE(:)
TYPE(D_MPS) PROBLEM
CHARACTER NAME*256
INTEGER I,J, K, NOUT
CALL UMACH(2, NOUT)
! READ LP PROBLEM FROM THE MPS FILE.
NAME = 'afiro'
CALL READ_MPS (NAME, PROBLEM)
ALLOCATE (A(PROBLEM%NROWS, PROBLEM%NCOLUMNS))
ALLOCATE (IRTYPE(PROBLEM%NROWS))
ALLOCATE (XSOL(PROBLEM%NCOLUMNS))
ALLOCATE (DSOL(PROBLEM%NROWS))
A = 0
IRTYPE = 3
! FILL DENSE A
DO K = 1, PROBLEM%NONZEROS
I = PROBLEM%CONSTRAINT(K)%ROW
J = PROBLEM%CONSTRAINT(K)%COLUMN
A(I,J) = PROBLEM%CONSTRAINT(K)%VALUE
ENDDO
! CALL THE LP SOLVER
CALL DENSE_LP (A, PROBLEM%LOWER_RANGE, PROBLEM%UPPER_RANGE, &
PROBLEM%OBJECTIVE, IRTYPE, OBJ, XSOL, DSOL, &
XLB=PROBLEM%LOWER_BOUND, XUB=PROBLEM%UPPER_BOUND)
WRITE(NOUT, 99999) OBJ
CALL WRRRN('Solution', XSOL, 1, PROBLEM%NROWS, 1)
DEALLOCATE(A)
DEALLOCATE(IRTYPE)
DEALLOCATE(XSOL)
DEALLOCATE(DSOL)
99999 FORMAT('Objective: ', E16.7)
END
Output
Objective: -0.4647531E+03
Solution
1 2 3 4 5 6 7 8 9 10
80.0 25.5 54.5 84.8 57.9 0.0 0.0 0.0 0.0 0.0
11 12 13 14 15 16 17 18 19 20
0.0 0.0 18.2 39.7 61.3 500.0 475.9 24.1 0.0 215.0
21 22 23 24 25 26 27
363.9 0.0 0.0 0.0 0.0 0.0 0.0
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |