This function computes the first, second or third derivative of a user-supplied function.

Function Return Value

DERIV — Estimate of the first (KORDER = 1), second (KORDER = 2) or third (KORDER = 3) derivative of FCN at X.   (Output)

Required Arguments

FCN — User-supplied FUNCTION whose derivative at X will be computed. The
form is FCN(X), where
                                X – Independent variable.   (Input)
                                FCN – The function value.   (Output)
FCN must be declared EXTERNAL in the calling program.

X — Point at which the derivative is to be evaluated.   (Input)

Optional Arguments

KORDER — Order of the derivative desired (1, 2 or 3).   (Input)
Default: KORDER = 1.

BGSTEP — Beginning value used to compute the size of the interval used in computing the derivative.   (Input)
The interval used is the closed interval (X − 4 * BGSTEP, X + 4 * BGSTEP). BGSTEP must be positive.
Default: BGSTEP = .01.

TOL — Relative error desired in the derivative estimate.   (Input)
Default: TOL = 1.e-2 for single precision and 1.d-4 for double precision.

FORTRAN 90 Interface

Generic:          DERIV (FCN, X [,…])

Specific:         The specific interface names are S_DERIV and D_DERIV.

FORTRAN 77 Interface

Single:            DERIV (FCN, KORDER, X, BGSTEP, TOL)

Double:          The double precision function name is DDERIV.

Description

DERIV produces an estimate to the first, second, or third derivative of a function. The estimate originates from first computing a spline interpolant to the input function using values within the interval (X − 4.0 * BGSTEP, X + 4.0 * BGSTEP), then differentiating the spline at X.

Comments

1.         Informational errors
Type                                   Code

   3                  2       Roundoff error became dominant before estimates converged. Increase precision and/or increase BGSTEP.

   4                  1       Unable to achieve desired tolerance in derivative estimation. Increase precision, increase TOL and/or change BGSTEP. If this error continues, the function may not have a derivative at X.

2.         Convergence is assumed when

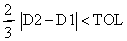
for two successive derivative estimates D1 and D2.

3.         The initial step size, BGSTEP, must be chosen small enough that FCN is defined and reasonably smooth in the interval (X − 4 * BGSTEP, X + 4 * BGSTEP), yet large enough to avoid roundoff problems.

Example 1

In this example, we obtain the approximate first derivative of the function

f(x) = −2 sin(3x/2)

at the point x = 2.

 

      USE DERIV_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

      INTEGER    KORDER, NCOUNT, NOUT

      REAL       BGSTEP, DERV, TOL, X

      EXTERNAL   FCN

!                                 Get output unit number

      CALL UMACH (2, NOUT)

!

      X      = 2.0

      BGSTEP = 0.2

      NCOUNT = 1

      DERV   = DERIV(FCN,X, BGSTEP=BGSTEP)

      WRITE (NOUT,99999) DERV

99999 FORMAT (/, 1X, 'First derivative of FCN is ', 1PE10.3)

      END

!

      REAL FUNCTION FCN (X)

      REAL       X

      REAL       SIN

      INTRINSIC  SIN

      FCN = -2.0*SIN(1.5*X)

      RETURN

      END

Output

 

First derivative of FCN is  2.970E+00

Additional Example

Example 2

In this example, we attempt to approximate in single precision the third derivative of the function

f(x) = 2x4 + 3x

at the point x = 0.75. Although the function is well-behaved near x = 0.75, finding derivatives is often computationally difficult on 32-bit machines. The difficulty is overcome in double precision.

 

      USE IMSL_LIBRARIES

 

      IMPLICIT   NONE

      INTEGER    KORDER, NOUT

      REAL       BGSTEP, DERV, X, TOL

      DOUBLE PRECISION DBGSTE, DDERV, DFCN, DTOL, DX

      EXTERNAL   DFCN, FCN

!                                 Get output unit number

      CALL UMACH (2, NOUT)

!                                 Turn off stopping due to error

!                                 condition

      CALL ERSET (0, -1, 0)

!

      X      = 0.75

      BGSTEP = 0.1

      KORDER = 3

!                                 In single precision, on a 32-bit

!                                 machine, the following attempt

!                                 produces an error message

      DERV = DERIV(FCN, X, KORDER, BGSTEP,TOL)

!                                 In double precision, we get good

!                                 results

      DX     = 0.75D0

      DBGSTE = 0.1D0

      DTOL   = 0.01D0

      KORDER = 3

      DDERV  = DERIV(DFCN, DX,KORDER, DBGSTE, DTOL)

      WRITE (NOUT,99999) DDERV

99999 FORMAT (/, 1X, 'The third derivative of DFCN is ', 1PD10.4)

      END

!

      REAL FUNCTION FCN (X)

      REAL       X

      FCN = 2.0*X**4 + 3.0*X

      RETURN

      END

!

      DOUBLE PRECISION FUNCTION DFCN (X)

      DOUBLE PRECISION X

      DFCN = 2.0D0*X**4 + 3.0D0*X

      RETURN

      END

Output

 

*** FATAL    ERROR 1 from DERIV.  Unable to achieve desired tolerance.
***          Increase precision, increase TOL = 1.000000E-02 and/or change
***          BGSTEP = 1.000000E-01.  If this error continues the function
***          may not have a derivative at X = 7.500000E-01

The third derivative of DFCN is 3.6000D+01

 

 

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260