This function computes the performance index for a real eigensystem.
Function Return Value
EPIRG — Performance index. (Output)
Required Arguments
NEVAL — Number of eigenvalue/eigenvector pairs on which the performance index computation is based. (Input)
A — Matrix of order N. (Input)
EVAL — Complex vector of length NEVAL containing eigenvalues of A. (Input)
EVEC — Complex
N by NEVAL array containing
eigenvectors of A. (Input)
The eigenvector corresponding to the eigenvalue EVAL(J) must be in the
J-th column of
EVEC.
Optional Arguments
N — Order of the
matrix A.
(Input)
Default: N = size
(A,2).
LDA — Leading
dimension of A
exactly as specified in the dimension statement in the calling
program. (Input)
Default: LDA = size
(A,1).
LDEVEC — Leading
dimension of EVEC exactly as
specified in the dimension statement in the calling program.
(Input)
Default: LDEVEC = size
(EVEC,1).
FORTRAN 90 Interface
Generic: EPIRG (NEVAL, A, EVAL, EVEC [,…])
Specific: The specific interface names are S_EPIRG and D_EPIRG.
FORTRAN 77 Interface
Single: EPIRG (N, NEVAL, A, LDA, EVAL, EVEC, LDEVEC)
Double: The double precision function name is DEPIRG.
Description
Let M = NEVAL, l = EVAL, xj = EVEC(*,J), the j-th column of EVEC. Also, let ε be the machine precision given by AMACH(4). The performance index, τ, is defined to be
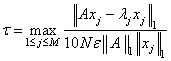
The norms used are a modified form of the 1-norm. The norm of the complex vector v is
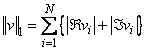
While the exact value of τ is highly machine dependent, the performance of EVCSF is considered excellent if τ < 1, good if 1 ≤ τ ≤ 100, and poor if τ > 100.
The performance index was first developed by the EISPACK project at Argonne National Laboratory; see Smith et al. (1976, pages 124− 125).
Comments
1. Workspace may be explicitly provided, if desired, by use of E2IRG/DE2IRG. The reference is:
E2IRG (N, NEVAL, A, LDA, EVAL, EVEC, LDEVEC, CWK)
The additional argument is:
CWK — Complex work array of length N.
2. Informational errors
Type Code
3 1 The performance index is greater than 100.
3 2 An eigenvector is zero.
3 3 The matrix is zero.
Example
For an example of EPIRG, see IMSL routine EVCRG.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |