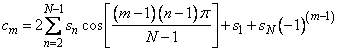Computes the discrete Fourier cosine transformation of an even sequence.

Required Arguments

N — Length of the sequence to be transformed. It must be greater than 1.   (Input)

SEQ — Array of length N containing the sequence to be transformed.   (Input)

COEF — Array of length N containing the transformed sequence.   (Output)

FORTRAN 90 Interface

Generic:          CALL FCOST (N, SEQ, COEF)

Specific:         The specific interface names are S_FCOST and D_FCOST.

FORTRAN 77 Interface

Single:            CALL FCOST (N, SEQ, COEF)

Double:          The double precision name is DFCOST.

Description

The routine FCOST computes the discrete Fourier cosine transform of a real vector of size N. The method used is a variant of the Cooley-Tukey algorithm , which is most efficient when N - 1 is a product of small prime factors. If N satisfies this condition, then the computational effort is proportional to N log N.

Specifically, given an N-vector s = SEQ, FCOST returns in c = COEF

Finally, note that the Fourier cosine transform is its own (unnormalized) inverse. Two applications of FCOST to a vector s produces (2N - 2)s. The routine FCOST is based on the cosine FFT in FFTPACK. The package FFTPACK was developed by Paul Swarztrauber at the National Center for Atmospheric Research.

Comments

1.         Workspace may be explicitly provided, if desired, by use of F2OST/DF2OST. The reference is:

CALL F2OST (N, SEQ, COEF, WFCOS)

The additional argument is

WFCOS — Array of length 3 * N + 15 initialized by FCOSI. The initialization depends on N.   (Input)

2.         The routine FCOST is most efficient when N - 1 is the product of small primes.

3.         The routine FCOST is its own (unnormalized) inverse. Applying FCOST twice will reproduce the original sequence multiplied by 2 * (N - 1).

4.         The arrays COEF and SEQ may be the same.

5.         If FCOST is used repeatedly with the same value of N, then call FCOSI followed by repeated calls to F2OST. This is more efficient than repeated calls to FCOST.

Example

In this example, we input a pure cosine wave as a data vector and recover its Fourier cosine series, which is a vector with all components zero except at the appropriate frequency it has an N - 1.

 

      USE FCOST_INT

      USE CONST_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

      INTEGER    N

      PARAMETER  (N=7)

!

      INTEGER    I, NOUT

      REAL       COEF(N), COS, FLOAT, PI, SEQ(N)

      INTRINSIC  COS, FLOAT

!

      CALL UMACH (2, NOUT)

!                                 Fill the data vector SEQ

!                                 with a pure cosine wave

      PI = CONST('PI')

      DO 10  I=1, N

         SEQ(I) = COS(FLOAT(I-1)*PI/FLOAT(N-1))

   10 CONTINUE

!                                 Compute the transform of SEQ

      CALL FCOST (N, SEQ, COEF)

!                                 Print results

      WRITE (NOUT,99998)

      WRITE (NOUT,99999) (I, SEQ(I), COEF(I), I=1,N)

99998 FORMAT (9X, 'INDEX', 6X, 'SEQ', 7X, 'COEF')

99999 FORMAT (1X, I11, 5X, F6.2, 5X, F6.2)

      END

Output

 

INDEX      SEQ       COEF
  1       1.00       0.00
  2       0.87       6.00
  3       0.50       0.00
  4       0.00       0.00
  5      -0.50       0.00
  6      -0.87       0.00
  7      -1.00       0.00

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260