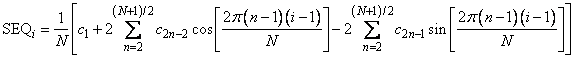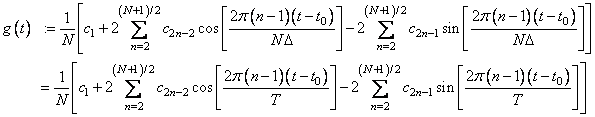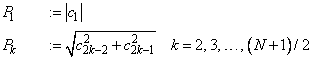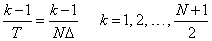Computes the Fourier coefficients of a real periodic sequence.
Required Arguments
N — Length of the sequence to be transformed. (Input)
SEQ — Array of length N containing the periodic sequence. (Input)
COEF — Array of length N containing the Fourier coefficients. (Output)
FORTRAN 90 Interface
Generic: CALL FFTRF (N, SEQ, COEF)
Specific: The specific interface names are S_FFTRF and D_FFTRF.
FORTRAN 77 Interface
Single: CALL FFTRF (N, SEQ, COEF)
Double: The double precision name is DFFTRF.
Description
The routine FFTRF computes the discrete Fourier transform of a real vector of size N. The method used is a variant of the Cooley-Tukey algorithm that is most efficient when N is a product of small prime factors. If N satisfies this condition, then the computational effort is proportional to N log N.
Specifically, given an N-vector s = SEQ, FFTRF returns in c = COEF, if N is even:
If N is odd, cm is defined as above for m from 2 to (N + 1)/2.
We now describe a fairly common usage of this routine. Let f be a real valued function of time. Suppose we sample f at N equally spaced time intervals of length Δ seconds starting at time t0. That is, we have
SEQ i:= f (t0 + (i - 1)Δ) i = 1, 2, …, N
The routine FFTRF treats this sequence as if it were periodic of period N. In particular, it assumes that f (t0) = f (t0 + NΔ). Hence, the period of the function is assumed to be T = NΔ.
Now, FFTRF accepts as input SEQ and returns as output coefficients c = COEF that satisfy the following relation when N is odd (N even is similar):
This formula is very revealing. It can be interpreted in the following manner. The coefficients produced by FFTRF produce an interpolating trigonometric polynomial to the data. That is, if we define
f(t0+ (i - 1)Δ) = g(t0 + (i - 1)Δ)
Now, suppose we want to discover the dominant frequencies. One forms the vector P of length N/2 as follows:
These numbers correspond to the energy in the spectrum of the signal. In particular, Pk corresponds to the energy level at frequency
Furthermore, note that there are only (N + 1)/2 ≈ T/(2Δ) resolvable frequencies when N observations are taken. This is related to the Nyquist phenomenon, which is induced by discrete sampling of a continuous signal.
Similar relations hold for the case when N is even.
Finally, note that the Fourier transform hsas an (unnormalized) inverse that is implemented in FFTRB. The routine FFTRF is based on the real FFT in FFTPACK. The package FFTPACK was developed by Paul Swarztrauber at the National Center for Atmospheric Research.
Comments
1. Workspace may be explicitly provided, if desired, by use of F2TRF/DF2TRF. The reference is:
CALL F2TRF (N, SEQ, COEF, WFFTR)
WFFTR —
Array of length 2N + 15 initialized by
FFTRI.
(Input)
The initialization depends on N.
2. The routine FFTRF is most efficient when N is the product of small primes.
3. The arrays COEF and SEQ may be the same.
4. If FFTRF/FFTRB is used repeatedly with the same value of N, then call FFTRI followed by repeated calls to F2TRF/F2TRB. This is more efficient than repeated calls to FFTRF/FFTRB.
Example
In this example, a pure cosine wave is used as a data vector, and its Fourier series is recovered. The Fourier series is a vector with all components zero except at the appropriate frequency where it has an N.
REAL COEF(N), COS, FLOAT, TWOPI, SEQ(N)
! This loop fills out the data vector
! with a pure exponential signal
SEQ(I) = COS(FLOAT(I-1)*TWOPI/FLOAT(N))
! Compute the Fourier transform of SEQ
99998 FORMAT (9X, 'INDEX', 5X, 'SEQ', 6X, 'COEF')
WRITE (NOUT,99999) (I, SEQ(I), COEF(I), I=1,N)
99999 FORMAT (1X, I11, 5X, F5.2, 5X, F5.2)
Output
INDEX
SEQ COEF
1
1.00 0.00
2 0.62
3.50
3 -0.22
0.00
4 -0.90
0.00
5 -0.90
0.00
6 -0.22
0.00
7
0.62 0.00
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |