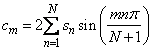Computes the discrete Fourier sine transformation of an odd sequence.

Required Arguments

N — Length of the sequence to be transformed. It must be greater than 1.   (Input)

SEQ — Array of length N containing the sequence to be transformed.   (Input)

COEF — Array of length N + 1 containing the transformed sequence.   (Output)

FORTRAN 90 Interface

Generic:         CALL FSINT (N, SEQ, COEF)

Specific:        The specific interface names are S_FSINT and D_FSINT.

FORTRAN 77 Interface

Single:            CALL FSINT (N, SEQ, COEF)

Double:          The double precision name is DFSINT.

Description

The routine FSINT computes the discrete Fourier sine transform of a real vector of size N. The method used is a variant of the Cooley-Tukey algorithm, which is most efficient when N + 1 is a product of small prime factors. If N satisfies this condition, then the computational effort is proportional to N log N.

Specifically, given an N-vector s = SEQ, FSINT returns in c = COEF

Finally, note that the Fourier sine transform is its own (unnormalized) inverse. The routine FSINT is based on the sine FFT in FFTPACK. The package FFTPACK was developed by Paul Swarztrauber at the National Center for Atmospheric Research.

Comments

1.         Workspace may be explicitly provided, if desired, by use of F2INT/DF2INT. The reference is:

CALL F2INT (N, SEQ, COEF, WFSIN)

The additional argument is:

WFSIN — Array of length INT(2.5 * N + 15) initialized by FSINI. The initialization depends on N.   (Input)

2.         The routine FSINT is most efficient when N + 1 is the product of small primes.

3.         The routine FSINT is its own (unnormalized) inverse. Applying FSINT twice will reproduce the original sequence multiplied by 2 * (N + 1).

4.         The arrays COEF and SEQ may be the same, if SEQ is also dimensioned at least N + 1.

5.         COEF (N + 1) is needed as workspace.

6.         If FSINT is used repeatedly with the same value of N, then call FSINI followed by repeated calls to F2INT. This is more efficient than repeated calls to FSINT.

Example

In this example, we input a pure sine wave as a data vector and recover its Fourier sine series, which is a vector with all components zero except at the appropriate frequency it has an N.

 

      USE FSINT_INT

      USE CONST_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

      INTEGER    N

      PARAMETER  (N=7)

!

      INTEGER    I, NOUT

      REAL       COEF(N+1), FLOAT, PI, SIN, SEQ(N)

      INTRINSIC  FLOAT, SIN

!                                 Get output unit number

      CALL UMACH (2, NOUT)

!                                 Fill the data vector SEQ

!                                 with a pure sine wave

      PI = CONST('PI')

      DO 10  I=1, N

         SEQ(I) = SIN(FLOAT(I)*PI/FLOAT(N+1))

   10 CONTINUE

!                                 Compute the transform of SEQ

      CALL FSINT (N, SEQ, COEF)

!                                 Print results

      WRITE (NOUT,99998)

      WRITE (NOUT,99999) (I, SEQ(I), COEF(I), I=1,N)

99998 FORMAT (9X, 'INDEX', 6X, 'SEQ', 7X, 'COEF')

99999 FORMAT (1X, I11, 5X, F6.2, 5X, F6.2)

      END

Output

 

INDEX      SEQ       COEF
  1       0.38       8.00
  2       0.71       0.00
  3       0.92       0.00
  4       1.00       0.00
  5       0.92       0.00
  6       0.71       0.00
  7       0.38       0.00

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260