Approximates the Hessian using forward differences and a user-supplied gradient.

Required Arguments

GRAD — User-supplied subroutine to compute the gradient at the point X. The usage is
CALL GRAD (N, X, G), where

N – Length of X and G.   (Input)

X – The point at which the gradient is evaluated.   (Input)
X should not be changed by GRAD.

G – The gradient evaluated at the point X.   (Output)

GRAD must be declared EXTERNAL in the calling program.

XC — Vector of length N containing the point at which the Hessian is to be estimated.   (Input)

GC — Vector of length N containing the gradient of the function at XC.   (Input)

H — N by N matrix containing the finite-difference approximation to the Hessian in the lower triangular part and diagonal.   (Output)

Optional Arguments

N — Dimension of the problem.   (Input)
Default: N = size (XC,1).

XSCALE — Vector of length N containing the diagonal scaling matrix for the variables.   (Input)
In the absence of other information, set all entries to 1.0.
Default: XSCALE = 1.0.

EPSFCN — Estimate of the relative noise in the function.   (Input)
EPSFCN must be less than or equal to 0.1. In the absence of other information, set EPSFCN to 0.0.
Default: EPSFCN = 0.0.

LDH — Leading dimension of H exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDH = size (H,1).

FORTRAN 90 Interface

Generic:          CALL GDHES (GRAD, XC, GC, H [,…])

Specific:         The specific interface names are S_GDHES and D_GDHES.

FORTRAN 77 Interface

Single:            CALL GDHES (GRAD, N, XC, XSCALE, GC, EPSFCN, H, LDH)

Double:          The double precision name is DGDHES.

Description

The routine GDHES uses the following finite-difference formula to estimate the Hessian matrix of function F at x:

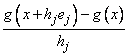
where hj = ɛ1/2 max{|xj|, 1/sj} sign(xj), ɛ is the machine epsilon, sj is the scaling factor of the j-th variable, g is the analytic gradient of F at x, and ej is the j-th unit vector. For more details, see Dennis and Schnabel (1983).

Since the finite-difference method has truncation error, cancellation error, and rounding error, users should be aware of possible poor performance. When possible, high precision arithmetic is recommended.

Comments

1.         Workspace may be explicitly provided, if desired, by use of G2HES/DG2HES. The reference is:

CALL G2HES (GRAD, N, XC, XSCALE, GC, EPSFCN, H, LDH, WK)

The additional argument is

WK — Work vector of length N.

2.         This is Description A5.6.1, Dennis and Schnabel, 1983; page 320.

Example

The Hessian is estimated by the finite-difference method at point (1.0, 1.0) from the following gradient functions:

 

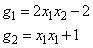
      USE GDHES_INT
      USE UMACH_INT

 

      IMPLICIT   NONE
!                                 Declaration of variables

      INTEGER    N, LDHES, NOUT

      PARAMETER  (N=2, LDHES=2)

      REAL       XC(N), GC(N), HES(LDHES,N)

      EXTERNAL   GRAD

!

      DATA XC/2*1.0E0/

!                                 Set function noise

!                                 Evaluate the gradient at the

!                                 current point

      CALL GRAD (N, XC, GC)

!                                 Get Hessian forward-difference

!                                 approximation

      CALL GDHES (GRAD, XC, GC, HES)

!

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) ((HES(I,J),J=1,N),I=1,N)

99999 FORMAT ('  THE HESSIAN IS', /, 2(5X,2F10.2,/),/)

!

      END

!

      SUBROUTINE GRAD (N, X, G)

!                                  SPECIFICATIONS FOR ARGUMENTS

      INTEGER N

      REAL    X(N), G(N)

!

      G(1) = 2.0E0*X(1)*X(2) - 2.0E0

      G(2) = X(1)*X(1) + 1.0E0

!

      RETURN

      END

Output

 

 THE HESSIAN IS
 2.00      2.00
 2.00      0.00

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260