Computes a Gauss, Gauss-Radau, or Gauss-Lobatto quadrature rule with various classical weight functions.
Required Arguments
N — Number of quadrature points. (Input)
QX — Array of length N containing quadrature points. (Output)
QW — Array of length N containing quadrature weights. (Output)
Optional Arguments
IWEIGH — Index of
the weight function. (Input)
Default: IWEIGH = 1.

ALPHA — Parameter
used in the weight function with some values of IWEIGH, otherwise it
is ignored. (Input)
Default: ALPHA =
2.0.
BETAW — Parameter
used in the weight function with some values of IWEIGH, otherwise it
is ignored. (Input)
Default: BETAW = 2.0.
NFIX — Number of
fixed quadrature points. (Input)
NFIX = 0, 1 or 2. For
the usual Gauss quadrature rules, NFIX = 0.
Default:
NFIX = 0.
QXFIX — Array of length NFIX (ignored if NFIX = 0) containing the preset quadrature point(s). (Input)
FORTRAN 90 Interface
Generic: CALL GQRUL (N, QX, QW [,…])
Specific: The specific interface names are S_GQRUL and D_GQRUL.
FORTRAN 77 Interface
Single: CALL GQRUL (N, IWEIGH, ALPHA, BETAW, NFIX, QXFIX, QX, QW)
Double: The double precision name is DGQRUL.
Description
The routine GQRUL produces the points and weights for the Gauss, Gauss-Radau, or Gauss-Lobatto quadrature formulas for some of the most popular weights. In fact, it is slightly more general than this suggests because the extra one or two points that may be specified do not have to lie at the endpoints of the interval. This routine is a modification of the subroutine GAUSSQUADRULE (Golub and Welsch 1969).
In the simple case when NFIX = 0, the routine returns points in x = QX and weights in w = QW so that
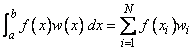
for all functions f that are polynomials of degree less than 2N.
If NFIX = 1, then one of the above xi equals the first component of QXFIX. Similarly, if NFIX = 2, then two of the components of x will equal the first two components of QXFIX. In general, the accuracy of the above quadrature formula degrades when NFIX increases. The quadrature rule will integrate all functions f that are polynomials of degree less than 2N − NFIX.
Comments
1. Workspace may be explicitly provided, if desired, by use of G2RUL/DG2RUL. The reference is
CALL G2RUL (N, IWEIGH, ALPHA, BETAW, NFIX, QXFIX, QX, QW, WK)
The additional argument is
WK — Work array of length N.
2. If IWEIGH specifies the weight WT(X) and the interval (a, b), then approximately
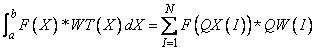
3. Gaussian quadrature is always the method of choice when the function F(X) behaves like a polynomial. Gaussian quadrature is also useful on infinite intervals (with appropriate weight functions), because other techniques often fail.
4. The weight function 1/cosh(X) behaves like a polynomial near zero and like e|X| far from zero.
Example 1
In this example, we obtain the classical Gauss-Legendre
quadrature formula, which is accurate for polynomials of degree less than
2N, and apply this when N = 6 to the function x8 on the interval
[−1, 1]. This
quadrature rule is accurate for polynomials of degree less than 12.
USE GQRUL_INT
USE UMACH_INT
IMPLICIT NONE
INTEGER N
PARAMETER (N=6)
INTEGER I, NOUT
REAL ANSWER, QW(N), QX(N), SUM
! Get output unit number
CALL UMACH (2, NOUT)
!
! Get points and weights from GQRUL
CALL GQRUL (N, QX, QW)
! Write results from GQRUL
WRITE (NOUT,99998) (I,QX(I),I,QW(I),I=1,N)
99998 FORMAT (6(6X,'QX(',I1,') = ',F8.4,7X,'QW(',I1,') = ',F8.5,/))
! Evaluate the integral from these
! points and weights
SUM = 0.0
DO 10 I=1, N
SUM = SUM + QX(I)**8*QW(I)
10 CONTINUE
ANSWER = SUM
WRITE (NOUT,99999) ANSWER
99999 FORMAT (/, ' The quadrature result making use of these ', &
'points and weights is ', 1PE10.4, '.')
END
Output
QX(1) = -0.9325
QW(1) = 0.17132
QX(2) =
-0.6612 QW(2) = 0.36076
QX(3)
= -0.2386 QW(3) =
0.46791
QX(4) = 0.2386 QW(4)
= 0.46791
QX(5) =
0.6612 QW(5) = 0.36076
QX(6)
= 0.9325 QW(6) =
0.17132
The quadrature result making use of these points and weights is
2.2222E-01.
Additional Examples
Example 2
We modify Example 1 by requiring that both endpoints be included in the quadrature formulas and again apply the new formulas to the function x8 on the interval [−1, 1]. This quadrature rule is accurate for polynomials of degree less than 10.
USE GQRUL_INT
USE UMACH_INT
IMPLICIT NONE
INTEGER N
PARAMETER (N=6)
INTEGER I, IWEIGH, NFIX, NOUT
REAL ALPHA, ANSWER, BETAW, QW(N), QX(N), QXFIX(2), SUM
! Get output unit number
CALL UMACH (2, NOUT)
!
IWEIGH = 1
ALPHA = 0.0
BETAW = 0.0
NFIX = 2
QXFIX(1) = -1.0
QXFIX(2) = 1.0
! Get points and weights from GQRUL
CALL GQRUL (N, QX, QW, ALPHA=ALPHA, BETAW=BETAW, NFIX=NFIX, &
QXFIX=QXFIX)
! Write results from GQRUL
WRITE (NOUT,99998) (I,QX(I),I,QW(I),I=1,N)
99998 FORMAT (6(6X,'QX(',I1,') = ',F8.4,7X,'QW(',I1,') = ',F8.5,/))
! Evaluate the integral from these
! points and weights
SUM = 0.0
DO 10 I=1, N
SUM = SUM + QX(I)**8*QW(I)
10 CONTINUE
ANSWER = SUM
WRITE (NOUT,99999) ANSWER
99999 FORMAT (/, ' The quadrature result making use of these ', &
'points and weights is ', 1PE10.4, '.')
END
Output
QX(1) = -1.0000
QW(1) = 0.06667
QX(2) =
-0.7651 QW(2) = 0.37847
QX(3)
= -0.2852 QW(3) =
0.55486
QX(4) = 0.2852 QW(4)
= 0.55486
QX(5) =
0.7651 QW(5) = 0.37847
QX(6)
= 1.0000 QW(6) =
0.06667
The quadrature result making use of these points and weights is
2.2222E-01.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |