The last two routines for interacting with the error handling system, IERCD and N1RTY, are INTEGER functions and are described in the following material.
IERCD retrieves the integer code for an informational error. Since it has no arguments, it may be used in the following way:
ICODE = IERCD( )
The function retrieves the code set by the most recently called IMSL routine.
N1RTY retrieves the error type set by the most recently called IMSL routine. It is used in the following way:
ITYPE = N1RTY(1)
ITYPE = 1, 2, 4, and 5 correspond to error severity levels 1, 2, 4, and 5, respectively. ITYPE = 3 and ITYPE = 6 are both warning errors, error severity level 3. While ITYPE = 3 errors are informational errors (IERCD( ) ≠ 0), ITYPE = 6 errors are not informational errors (IERCD( ) = 0).
For software developers requiring additional interaction with the IMSL error handling system, see Aird and Howell (1991).
Examples
Changes to default actions
Some possible changes to the default actions are illustrated below. The default actions remain in effect for the kinds of errors not included in the call to ERSET.
To turn off printing of warning
error messages:
CALL
ERSET (3, 0, −1)
To stop if warning errors
occur:
CALL
ERSET (3, −1, 1)
To print all error
messages:
CALL
ERSET (0, 1, −1)
To restore all default
settings:
CALL
ERSET (0, 2, 2)
Use of informational error to determine program action
In the program segment below, the Cholesky factorization of a matrix is to be performed. If it is determined that the matrix is not nonnegative definite (and often this is not immediately obvious), the program is to take a different branch.
.
.
.
CALL LFTDS (A,
FACT)
IF (IERCD() .EQ. 2)
THEN
!
Handle matrix that is not nonnegative
definite
.
.
.
END IF
Examples of errors
The program below illustrates each of the different types of errors detected by the MATH/LIBRARY routines.
The error messages refer to the argument names that are used in the documentation for the routine, rather than the user's name of the variable used for the argument. In the message generated by IMSL routine LINRG in this example, reference is made to N, whereas in the program a literal was used for this argument.
USE_IMSL_LIBRARIES
INTEGER
N
PARAMETER (N=2)
!
REAL A(N,N), AINV(N,N), B(N), X(N)
!
DATA A/2.0, -3.0, 2.0, -3.0/
DATA B/1.0, 2.0/
! Turn on printing and turn off
! stopping for all error types.
CALL ERSET (0, 1, 0)
! Generate level 4 informational error.
CALL LSARG (A, B, X)
! Generate level 5 terminal error.
CALL LINRG (A, AINV, N = -1)
END
Output
*** FATAL ERROR 2 from LSARG. The
input matrix is singular. Some of
*** the diagonal
elements of the upper triangular matrix U of the
*** LU factorization
are close to zero.
*** TERMINAL ERROR 1 from LINRG. The order of
the matrix must be
positive
*** while N =
−1 is
given.
Example of traceback
The next program illustrates a situation in which a traceback is produced. The program uses the IMSL quadrature routines QDAG and QDAGS to evaluate the double integral
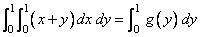
where
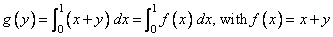
Since both QDAG and QDAGS need 2500 numeric storage units of workspace, and since the workspace allocator uses some space to keep track of the allocations, 6000 numeric storage units of space are explicitly allocated for workspace. Although the traceback shows an error code associated with a terminal error, this code has no meaning to the user; the printed message contains all relevant information. It is not assumed that the user would take corrective action based on knowledge of the code.
USE
QDAGS_INT
!
Specifications for local variables
REAL A, B, ERRABS, ERREST, ERRREL, G, RESULT
EXTERNAL G
! Set quadrature parameters
A = 0.0
B = 1.0
ERRABS = 0.0
ERRREL = 0.001
! Do the outer integral
CALL QDAGS (G, A, B, RESULT, ERRABS, ERRREL, ERREST)
!
WRITE (*,*) RESULT, ERREST
END
!
REAL FUNCTION G
(ARGY)
USE QDAG_INT
REAL ARGY
!
INTEGER IRULE
REAL C, D, ERRABS, ERREST, ERRREL, F, Y
COMMON /COMY/ Y
EXTERNAL F
!
Y = ARGY
C = 0.0
D = 1.0
ERRABS = 0.0
ERRREL = -0.001
IRULE = 1
!
CALL QDAG (F, C, D, G, ERRABS, ERRREL, IRULE, ERREST)
RETURN
END
!
REAL FUNCTION F (X)
REAL X
!
REAL Y
COMMON /COMY/ Y
!
F = X + Y
RETURN
END
Output
*** TERMINAL ERROR 4 from Q2AG. The relative error desired ERRREL =
*** -1.000000E-03. It must be at least zero.
Here is a traceback of subprogram calls in reverse order:
Routine name Error type Error code
------------ ---------- ----------
Q2AG 5 4 (Called internally)
QDAG 0 0
Q2AGS 0 0 (Called internally)
QDAGS 0 0
USER 0 0
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |