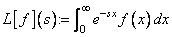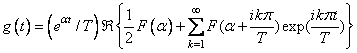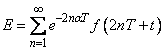Computes the inverse Laplace transform of a complex function.

Required Arguments

F — User-supplied FUNCTION to which the inverse Laplace transform will be computed. The form is F(Z), where

            Z – Complex argument.   (Input)
F – The complex function value.   (Output)

F must be declared EXTERNAL in the calling program. F should also be declared COMPLEX.

T — Array of length N containing the points at which the inverse Laplace transform is desired.   (Input)
T(I) must be greater than zero for all I.

FINV — Array of length N whose I-th component contains the approximate value of the Laplace transform at the point T(I).   (Output)

Optional Arguments

N — Number of points at which the inverse Laplace transform is desired.   (Input)
Default: N = size (T,1).

ALPHA — An estimate for the maximum of the real parts of the singularities of F. If unknown, set ALPHA = 0.   (Input)
Default: ALPHA = 0.0.

KMAX — The number of function evaluations allowed for each T(I).   (Input)
Default: KMAX = 500.

RELERR — The relative accuracy desired.   (Input)
Default: RELERR = 1.1920929e-5 for single precision and 2.22d-10 for double precision.

FORTRAN 90 Interface

Generic:          CALL INLAP (F, T, FINV [,…])

Specific:         The specific interface names are S_INLAP and D_INLAP.

FORTRAN 77 Interface

Single:            CALL INLAP (F, N, T, ALPHA, RELERR, KMAX, FINV)

Double:          The double precision name is DINLAP.

Description

The routine INLAP computes the inverse Laplace transform of a complex-valued function. Recall that if f is a function that vanishes on the negative real axis, then we can define the Laplace transform of f by

It is assumed that for some value of s the integrand is absolutely integrable.

The computation of the inverse Laplace transform is based on applying the epsilon algorithm to the complex Fourier series obtained as a discrete approximation to the inversion integral. The initial algorithm was proposed by K.S. Crump (1976) but was significantly improved by de Hoog et al. (1982). Given a complex-valued transform F(s) = L[f](s), the trapezoidal rule gives the approximation to the inverse transform

This is the real part of the sum of a complex power series in z = exp(i πt/T), and the algorithm accelerates the convergence of the partial sums of this power series by using the epsilon algorithm to compute the corresponding diagonal Pade approximants. The algorithm attempts to choose the order of the Pade approximant to obtain the specified relative accuracy while not exceeding the maximum number of function evaluations allowed. The parameter α is an estimate for the maximum of the real parts of the singularities of F, and an incorrect choice of α may give false convergence. Even in cases where the correct value of α is unknown, the algorithm will attempt to estimate an acceptable value. Assuming satisfactory convergence, the discretization error
E := g - f satisfies

It follows that if |f(t)| ≤ Meβt, then we can estimate the expression above to obtain
(for 0 ≤ t ≤ 2T)

Comments

Informational errors
Type           Code

   4                    1     The algorithm was not able to achieve the accuracy requested within KMAX       function evaluations for some T(I).

   4                    2     Overflow is occurring for a particular value of T.

Example

We invert the Laplace transform of the simple function (s - 1)-2 and print the computed answer, the true solution and the difference at five different points. The correct inverse transform is xex.

 

      USE INLAP_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

      INTEGER    I, KMAX, N, NOUT

      REAL       ALPHA, DIF(5), EXP, FINV(5), FLOAT, RELERR, T(5), &

                TRUE(5)

      COMPLEX    F

      INTRINSIC  EXP, FLOAT

      EXTERNAL   F

!                                 Get output unit number

      CALL UMACH (2, NOUT)

!

      DO 10  I=1, 5

         T(I) = FLOAT(I) - 0.5

   10 CONTINUE

      N      = 5

      ALPHA  = 1.0E0

      RELERR = 5.0E-4

      CALL INLAP (F, T, FINV, ALPHA=ALPHA, RELERR=RELERR)

!                                 Evaluate the true solution and the

!                                 difference

      DO 20  I=1, 5

         TRUE(I) = T(I)*EXP(T(I))

         DIF(I) = TRUE(I) - FINV(I)

   20 CONTINUE

!

      WRITE (NOUT,99999) (T(I),FINV(I),TRUE(I),DIF(I),I=1,5)

99999 FORMAT (7X, 'T', 8X, 'FINV', 9X, 'TRUE', 9X, 'DIFF', /, &

            5(1X,E9.1,3X,1PE10.3,3X,1PE10.3,3X,1PE10.3,/))

      END

!

      COMPLEX FUNCTION F (S)

      COMPLEX    S

      F = 1./(S-1.)**2

      RETURN

      END

Output

 

    T        FINV         TRUE         DIFF
0.5E+00    8.244E-01    8.244E-01   -4.768E-06
1.5E+00    6.723E+00    6.723E+00   -3.481E-05
2.5E+00    3.046E+01    3.046E+01   -1.678E-04
3.5E+00    1.159E+02    1.159E+02   -6.027E-04
4.5E+00    4.051E+02    4.051E+02   -2.106E-03

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260