Minimizes a general objective function subject to linear equality/inequality constraints.
Required Arguments
FCN — User-supplied subroutine to evaluate the function to be minimized. The usage is CALL FCN (N, X, F), where
N – Value of NVAR. (Input)
X – Vector of length
N at which point
the function is evaluated. (Input)
X should not be
changed by FCN.
F – The computed function value at the point X. (Output)
FCN must be declared EXTERNAL in the calling program.
GRAD —
User-supplied subroutine to compute the gradient at the point X. The usage is
CALL GRAD
(N, X,
G),
where
N –
Value of NVAR.
(Input)
X – Vector of length
N at which point
the function is evaluated. (Input)
X should not be
changed by GRAD.
G – Vector of length N containing the values of the gradient of the objective function evaluated at the point X. (Output)
GRAD must be declared EXTERNAL in the calling program.
NEQ — The number of linear equality constraints. (Input)
A — NCON by NVAR
matrix. (Input)
The matrix contains the equality constraint
gradients in the first NEQ rows, followed by
the inequality constraint gradients.
B — Vector of
length NCON
containing right-hand sides of the linear constraints. (Input)
Specifically, the constraints on the variables X(I), I = 1, …, NVAR are
A(K, 1) * X(1) + … + A(K, NVAR) * X(NVAR).EQ.B(K), K = 1, …,
NEQ.A(K, 1) * X(1) + … + A(K, NVAR) * X(NVAR).LE.B(K), K = NEQ + 1, …, NCON. Note that the
data that define the equality constraints come before the data of the
inequalities.
XLB — Vector of
length NVAR
containing the lower bounds on the variables; choose a very large negative value
if a component should be unbounded below or set
XLB(I) = XUB(I) to freeze the I-th
variable. (Input)
Specifically, these simple bounds are XLB(I).LE.X(I), I = 1, …, NVAR.
XUB — Vector of
length NVAR
containing the upper bounds on the variables; choose a very large positive value
if a component should be unbounded above. (Input)
Specifically,
these simple bounds are X(I).LE. XUB(I), I = 1, …, NVAR.
SOL — Vector of length NVAR containing solution. (Output)
Optional Arguments
NVAR — The number
of variables. (Input)
Default: NVAR = size
(A,2).
NCON — The number
of linear constraints (excluding simple bounds). (Input)
Default:
NCON = size
(A,1).
LDA — Leading
dimension of A
exactly as specified in the dimension statement of the calling
program. (Input)
Default: LDA = size
(A,1).
XGUESS — Vector
of length NVAR
containing the initial guess of the minimum. (Input)
Default:
XGUESS =
0.0.
ACC — The
nonnegative tolerance on the first order conditions at the calculated
solution. (Input)
Default: ACC = 1.e-4 for single
precision and 1.d-8 for double precision.
MAXFCN — On
input, maximum number of function evaluations allowed.(Input/ Output)
On
output, actual number of function evaluations needed.
Default: MAXFCN = 400.
OBJ — Value of the objective function. (Output)
NACT — Final number of active constraints. (Output)
IACT — Vector
containing the indices of the final active constraints in the first NACT
positions. (Output)
Its length must be at least NCON + 2 * NVAR.
ALAMDA — Vector of length NVAR containing the Lagrange multiplier estimates of the final active constraints in the first NACT positions. (Output)
FORTRAN 90 Interface
Generic: CALL LCONG (FCN, GRAD, NEQ, A, B, XLB, XUB, SOL [,…])
Specific: The specific interface names are S_LCONG and D_LCONG.
FORTRAN 77 Interface
Single: CALL LCONG (FCN, GRAD, NVAR, NCON, NEQ, A, LDA, B, XLB, XUB, XGUESS, ACC, MAXFCN, SOL, OBJ, NACT, IACT, ALAMDA)
Double: The double precision name is DLCONG.
Description
The routine LCONG is based on M.J.D. Powell's TOLMIN, which solves linearly constrained optimization problems, i.e., problems of the form
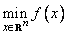
subject to A1x = b1
A2x ≤ b2
xl ≤ x ≤ xu
given the vectors b1, b2, xl and xu and the matrices A1, and A2.
The algorithm starts by checking the equality constraints for inconsistency and redundancy. If the equality constraints are consistent, the method will revise x0, the initial guess provided by the user, to satisfy
A1x = b1
Next, x0 is adjusted to satisfy the simple bounds and inequality constraints. This is done by solving a sequence of quadratic programming subproblems to minimize the sum of the constraint or bound violations.
Now, for each iteration with a feasible xk, let Jk be the set of indices of inequality constraints that have small residuals. Here, the simple bounds are treated as inequality constraints. Let Ik be the set of indices of active constraints. The following quadratic programming problem
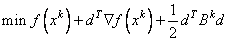
subject to ajd = 0 j ∈ Ik
ajd ≤ 0 j ∈ Jk
is solved to get (dk, λk) where aj is a row vector
representing either a constraint in A1or A2 or a bound constraint
on x. In the latter case, the aj = ei for the bound
constraint xi ≤ (xu)i and
aj = - ei for the constraint
- xi ≤ ( - xl)i. Here, ei is a vector with a 1
as the i-th component, and zeroes elsewhere. λk are the Lagrange
multipliers, and Bk is a positive definite
approximation to the second derivative ∇2f(xk).
After the search direction dk is obtained, a line search is performed to locate a better point. The new point xk+1= xk + αkdk has to satisfy the conditions
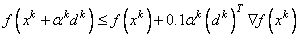
and
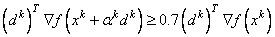
The main idea in forming the set Jk is that, if any of the inequality constraints restricts the step-length αk, then its index is not in Jk. Therefore, small steps are likely to be avoided.
Finally, the second derivative approximation, Bk, is updated by the BFGS formula, if the condition
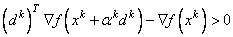
holds. Let xk ← xk+1, and start another iteration.
The iteration repeats until the stopping criterion
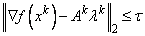
is satisfied; here, τ is a user-supplied tolerance. For more details, see Powell (1988, 1989).
Comments
1. Workspace may be explicitly provided, if desired, by use of L2ONG/DL2ONG. The reference is:
CALL L2ONG (FCN, GRAD, NVAR, NCON, NEQ, A, LDA, B, XLB, XUB, XGUESS, ACC, MAXFCN, SOL, OBJ, NACT, IACT, ALAMDA, IPRINT, INFO, WK)
The additional arguments are as follows:
IPRINT — Print option (see Comment 3). (Input)
INFO — Informational flag (see Comment 3). (Output)
WK — Real work vector of length NVAR**2 + 11 * NVAR + NCON.
2. Informational errors
Type Code
4 4 The equality constraints are inconsistent.
4 5 The equality constraints and the bounds on the variables are found to be inconsistent.
4 6 No vector X satisfies all of the constraints. In particular, the current active constraints prevent any change in X that reduces the sum of constraint violations.
4 7 Maximum number of function evaluations exceeded.
4 9 The variables are determined by the equality constraints.
3. The following are descriptions of the arguments IPRINT and INFO:
IPRINT —
This argument must be set by the user to specify the frequency of printing
during the execution of the routine LCONG. There is no printed output if
IPRINT =
0. Otherwise, after ensuring feasibility, information is given every IABS(IPRINT) iterations
and whenever a parameter called TOL is reduced. The printing provides the
values of X(.), F(.) and G(.) = GRAD(F) if IPRINT is positive. If IPRINT is
negative, this information is augmented by the current values of IACT(K) K = 1, …, NACT, PAR(K) K = 1, …, NACT and
RESKT(I) I = 1, …,
N. The
reason for returning to the calling program is also displayed when IPRINT is
nonzero.
INFO — On exit
from L2ONG,
INFO will
have one of the following integer
values to indicate the reason for leaving the routine:
INFO =
1 SOL is feasible and
the condition that depends on ACC is
satisfied.
INFO =
2 SOL is feasible and
rounding errors are preventing further progress.
INFO =
3 SOL is feasible but
the objective function fails to decrease although
a decrease is predicted by the current gradient vector.
INFO =
4 In this
case, the calculation cannot begin because LDA is less than
NCON or because
the lower bound on a variable is greater than the
upper bound.
INFO =
5 This value
indicates that the equality constraints are inconsistent.
These constraints include any components of X(.) that are frozen
by setting XL(I) = XU(I).
INFO =
6 In this
case, there is an error return because the equality constraints
and the bounds on the variables are found to be inconsistent.
INFO =
7 This value
indicates that there is no vector of variables that
satisfies all of the constraints. Specifically, when this return or an
INFO = 6 return
occurs, the current active constraints (whose
indices are IACT(K), K = 1, …, NACT) prevent any
change in X(.)
that reduces the sum of constraint violations, where only bounds
are included in this sum if INFO = 6.
INFO =
8 Maximum
number of function evaluations exceeded.
INFO =
9 The
variables are determined by the equality constraints.
Example
The problem from Schittkowski (1987)
min f(x) = - x1 x2 x3
subject to - x1 - 2x2 - 2x3 ≤ 0
x1 +2 x2 + 2 x3 ≤ 72
0 ≤ x1 ≤ 20
0 ≤ x2 ≤ 11
0 ≤ x3 ≤ 42
is solved with an initial guess x1 = 10, x2= 10 and x3 = 10.
USE LCONG_INT
USE UMACH_INT
IMPLICIT NONE
! Declaration of variables
INTEGER NCON, NEQ, NVAR
PARAMETER (NCON=2, NEQ=0, NVAR=3)
!
INTEGER MAXFCN, NOUT
REAL A(NCON,NVAR), ACC, B(NCON), OBJ, &
SOL(NVAR), XGUESS(NVAR), XLB(NVAR), XUB(NVAR)
EXTERNAL FCN, GRAD
!
! Set values for the following problem.
!
! Min -X(1)*X(2)*X(3)
!
! -X(1) - 2*X(2) - 2*X(3) .LE. 0
! X(1) + 2*X(2) + 2*X(3) .LE. 72
!
! 0 .LE. X(1) .LE. 20
! 0 .LE. X(2) .LE. 11
! 0 .LE. X(3) .LE. 42
!
DATA A/-1.0, 1.0, -2.0, 2.0, -2.0, 2.0/, B/0.0, 72.0/
DATA XLB/3*0.0/, XUB/20.0, 11.0, 42.0/, XGUESS/3*10.0/
DATA ACC/0.0/, MAXFCN/400/
!
CALL UMACH (2, NOUT)
!
CALL LCONG (FCN, GRAD, NEQ, A, B, XLB, XUB, SOL, XGUESS=XGUESS, &
ACC=ACC, MAXFCN=MAXFCN, OBJ=OBJ)
!
WRITE (NOUT,99998) 'Solution:'
WRITE (NOUT,99999) SOL
WRITE (NOUT,99998) 'Function value at solution:'
WRITE (NOUT,99999) OBJ
WRITE (NOUT,99998) 'Number of function evaluations:', MAXFCN
STOP
99998 FORMAT (//, ' ', A, I4)
99999 FORMAT (1X, 5F16.6)
END
!
SUBROUTINE FCN (N, X, F)
INTEGER N
REAL X(*), F
!
F = -X(1)*X(2)*X(3)
RETURN
END
!
SUBROUTINE GRAD (N, X, G)
INTEGER N
REAL X(*), G(*)
!
G(1) = -X(2)*X(3)
G(2) = -X(1)*X(3)
G(3) = -X(1)*X(2)
RETURN
END
Output
Solution:
20.000000
11.000000 15.000000
Function value at
solution:
-3300.000000
Number of function evaluations:
5
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |