Computes the determinant of a complex triangular matrix.

Required Arguments

A — Complex N by N matrix containing the triangular matrix.(Input)

DET1 — Complex scalar containing the mantissa of the determinant.   (Output)
The value DET1 is normalized so that 1.0 ≤ ½DET1½ <10.0 or DET1= 0.0.

DET2 — Scalar containing the exponent of the determinant.   (Output)
The determinant is returned in the form det(A) = DET1 *10^DET2.

Optional Arguments

N — Number of equations.   (Input)
Default: N = size (A,2).

LDA — Leading dimension of A exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDA = size (A,1).

FORTRAN 90 Interface

Generic:                              CALL LFDCT (A, DET1, DET2[,…])

Specific:                             The specific interface names are S_LFDCT and D_LFDCT.

FORTRAN 77 Interface

Single:                                CALL LFDCT (N, A, LDA, DET1, DET2)

Double:                              The double precision name is DLFDCT.

Description

Routine LFDCT computes the determinant of a complex triangular coefficient matrix. The determinant of a triangular matrix is the product of the diagonal elements

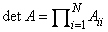
LFDCT is based on the LINPACK routine CTRDI; see Dongarra et al. (1979).

Comments

Informational error

Type       Code

3                   1                     The input triangular matrix is singular.

Example

The determinant is computed for a 3 × 3 complex lower triangular matrix.

 

      USE LFDCT_INT
      USE UMACH_INT

!                                 Declare variables

      INTEGER    LDA, N

      PARAMETER  (LDA=3, N=3)

      INTEGER    NOUT

      REAL       DET2

      COMPLEX    A(LDA,LDA), DET1

!                                Set values for A

!

!                                A = ( -3.0+2.0i                     )

!                                    ( -2.0-1.0i  0.0+6.0i           )

!                                    ( -1.0+3.0i  1.0-5.0i -4.0+0.0i )

!

      DATA A/(-3.0,2.0), (-2.0,-1.0), (-1.0, 3.0), (0.0,0.0), (0.0,6.0),&

            (1.0,-5.0), (0.0,0.0), (0.0,0.0), (-4.0,0.0)/

!

!                                 Compute the determinant of A

      CALL LFDCT (A, DET1, DET2)

!                                 Print results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) DET1, DET2

99999 FORMAT (' The determinant of A is (',F4.1,',',F4.1,') * 10**',&

             F2.0)

      END

Output

 

The determinant of A is ( 0.5, 0.7) * 10**2.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260