Computes the determinant of a complex Hermitian positive definite matrix given the RHR Cholesky factorization in band Hermitian storage mode.

Required Arguments

FACT — Complex NCODA + 1 by N array containing the RHR factorization of the Hermitian positive definite band matrix A.   (Input)
FACT is obtained as output from routine LFCQH/DLFCQH or LFTQH/DLFTQH.

NCODA — Number of upper or lower codiagonals of A.   (Input)

DET1 — Scalar containing the mantissa of the determinant.   (Output)
The value DET1 is normalized so that 1.0 ≤ ǀDET1 ǀ < 10.0 or DET1 = 0.0.

DET2 — Scalar containing the exponent of the determinant.   (Output)
The determinant is returned in the form det (A) = DET1 * 10^DET2.

Optional Arguments

N — Number of equations.   (Input)
Default: N = size (FACT,2).

LDFACT — Leading dimension of FACT exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDFACT = size (FACT,1).

FORTRAN 90 Interface

Generic:                              CALL LFDQH (FACT, NCODA, DET1, DET2 [,…])

Specific:                             The specific interface names are S_LFDQH and D_LFDQH.

FORTRAN 77 Interface

Single:            CALL LFDQH (N, FACT, LDFACT, NCODA, DET1, DET2)

Double:                              The double precision name is DLFDQH.

Description

Routine LFDQH computes the determinant of a complex Hermitian positive definite band coefficient matrix. To compute the determinant, the coefficient matrix must first undergo an
RH R factorization. This may be done by calling either LFCQH or LFTQH. The formula
det A = det RH det R = (det R)2 is used to compute the determinant. Since the determinant of a triangular matrix is the product of the diagonal elements,

 

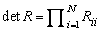
LFDQH is based on the LINPACK routine CPBDI; see Dongarra et al. (1979).

Example

The determinant is computed for a 5 × 5 complex Hermitian positive definite band matrix with one codiagonal.

 

      USE LFDQH_INT
      USE LFTQH_INT
      USE UMACH_INT
!                                 Declare variables

      INTEGER    LDA, LDFACT, N, NCODA, NOUT

      PARAMETER  (LDA=2, N=5, LDFACT=2, NCODA=1)

      REAL       DET1, DET2

      COMPLEX    A(LDA,N), FACT(LDFACT,N)

!

!            Set values for A in band Hermitian form

!

!            A = ( 0.0+0.0i -1.0+1.0i  1.0+2.0i  0.0+4.0i  1.0+1.0i )

!                ( 2.0+0.0i  4.0+0.0i 10.0+0.0i  6.0+0.0i  9.0+0.0i )

!

      DATA A/(0.0,0.0), (2.0,0.0), (-1.0,1.0), (4.0, 0.0), (1.0,2.0),&

            (10.0,0.0), (0.0,4.0), (6.0,0.0), (1.0,1.0), (9.0,0.0)/

!                                 Factor the matrix

      CALL LFTQH (A, NCODA, FACT)

!                                 Compute the determinant

      CALL LFDQH (FACT, NCODA, DET1, DET2)

!                                 Print results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) DET1, DET2

!

99999 FORMAT (' The determinant of A is ',F6.3,' * 10**',F2.0)

      END

Output

 

The determinant of A is  1.736 * 10**3.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260