Solves a sparse system of linear equations given the LU factorization of the coefficient matrix..
Required Arguments
NFAC — The number of nonzero coefficients in FACT as output from subroutine LFTXG/DLFTXG. (Input)
NL — The number of nonzero coefficients in the triangular matrix L excluding the diagonal elements as output from subroutine LFTXG/DLFTXG. (Input)
FACT — Vector of length NFAC containing the nonzero elements of L (excluding the diagonals) in the first NL locations and the nonzero elements of U in NL + 1 to NFAC locations as output from subroutine LFTXG/DLFTXG. (Input)
IRFAC — Vector of length NFAC containing the row numbers of the corresponding elements in FACT as output from subroutine LFTXG/DLFTXG. (Input)
JCFAC — Vector of length NFAC containing the column numbers of the corresponding elements in FACT as output from subroutine LFTXG/DLFTXG. (Input)
IPVT — Vector of length N containing the row pivoting information for the LU factorization as output from subroutine LFTXG/DLFTXG. (Input)
JPVT — Vector of length N containing the column pivoting information for the LU factorization as output from subroutine LFTXG/DLFTXG. (Input)
B — Vector of length N containing the right-hand side of the linear system. (Input)
X — Vector of length N containing the solution to the linear system. (Output)
Optional Arguments
N — Number of equations.
(Input)
Default: N = size (B,1).
IPATH — Path indicator. (Input)
IPATH = 1
means the system Ax = B is solved.
IPATH = 2 means the
system ATx = B is solved.
Default:
IPATH = 1.
FORTRAN 90 Interface
Generic: CALL LFSXG (NFAC, NL, FACT, IRFAC, JCFAC, IPVT, JPVT, B, X [,…])
Specific: The specific interface names are S_LFSXG and D_LFSXG.
FORTRAN 77 Interface
Single: CALL LFSXG (N, NFAC, NL, FACT, IRFAC, JCFAC, IPVT, JPVT, B, IPATH, X)
Double: The double precision name is DLFSXG.
Description
Consider the linear equation
Ax = b
where A is a n× n sparse matrix. The sparse coordinate format for the matrix A requires one real and two integer vectors. The real array a contains all the nonzeros in A. Let the number of nonzeros be nz. The two integer arrays irow and jcol, each of length nz, contain the row and column numbers for these entries in A. That is
Airow(i),icol(i) = a(i), i = 1, …, nz
with all other entries in A zero. The routine LFSXG computes the solution of the linear equation given its LU factorization. The factorization is performed by calling LFTXG. The solution of the linear system is then found by the forward and backward substitution. The algorithm can be expressed as
P AQ = LU
where P and Q are the row and column permutation matrices determined by the Markowitz strategy (Duff et al. 1986), and L and U are lower and upper triangular matrices, respectively. Finally, the solution x is obtained by the following calculations:
1) Lz = Pb
2) Uy = z
3) x = Qy
For more details, see Crowe et al. (1990).
Example
As an example, consider the 6 × 6 linear system:

Let
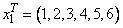
so that Ax1 = (10, 7, 45, 33,−34, 31)T, and
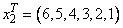
so that Ax2 = (60, 35, 60, 16, −22, 10)T. The sparse coordinate form for A is given by:
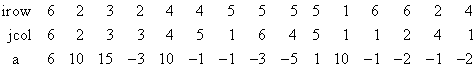
USE
LFSXG_INT
USE
WRRRL_INT
USE LFTXG_INT
INTEGER N, NZ
PARAMETER (N=6, NZ=15)
INTEGER IPATH, IROW(NZ), JCOL(NZ), NFAC,&
NL, IRFAC(3*NZ), JCFAC(3*NZ), IPVT(N), JPVT(N)
REAL X(N), A(NZ), B(N,2), FACT(3*NZ)
CHARACTER TITLE(2)*2, RLABEL(1)*4, CLABEL(1)*6
DATA RLABEL(1)/'NONE'/, CLABEL(1)/'NUMBER'/
!
DATA A/6., 10., 15., -3., 10., -1., -1., -3., -5., 1., 10., -1.,&
-2., -1., -2./
DATA B/10., 7., 45., 33., -34., 31.,&
60., 35., 60., 16., -22., -10./
DATA IROW/6, 2, 3, 2, 4, 4, 5, 5, 5, 5, 1, 6, 6, 2, 4/
DATA JCOL/6, 2, 3, 3, 4, 5, 1, 6, 4, 5, 1, 1, 2, 4, 1/
DATA TITLE/'x1', 'x2'/
!
NFAC = 3*NZ
! Perform LU factorization
CALL LFTXG (A, IROW, JCOL, NL, NFAC, FACT, IRFAC, JCFAC, IPVT, JPVT)
!
DO 10 I = 1, 2
! Solve A * X(i) = B(i)
CALL LFSXG (NFAC, NL, FACT, IRFAC, JCFAC, IPVT, JPVT, B(:,I), X)
!
CALL WRRRL (TITLE(I), X, RLABEL, CLABEL, 1, N, 1)
10 CONTINUE
END
Output
x1
1 2
3 4 5
6
1.0 2.0 3.0 4.0
5.0 6.0
x2
1 2 3 4 5 6
6.0 5.0 4.0 3.0 2.0 1.0
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |