Solves a complex sparse Hermitian positive definite system of linear equations, given the Cholesky factorization of the coefficient matrix.
Required Arguments
N — Number of equations. (Input)
MAXSUB — Number of subscripts contained in array NZSUB as output from subroutine LSCXD/DLSCXD. (Input)
NZSUB — Vector of length MAXSUB containing the row subscripts for the off-diagonal nonzeros in the factor as output from subroutine LSCXD/DLSCXD. (Input)
INZSUB — Vector of length N + 1 containing
pointers for NZSUB as output from
subroutine LSCXD/DLSCXD.
(Input)
The row subscripts of column J are stored from
location INZSUB(J) to
INZSUB(J + 1) − 1.
MAXNZ — Total number of off-diagonal nonzeros in the Cholesky factor as output from subroutine LSCXD/DLSCXD. (Input)
RLNZ — Complex vector of length MAXNZ containing the off-diagonal nonzeros in the factor in column ordered format as output from subroutine LNFZD/DLNFZD. (Input)
ILNZ — Vector of length N +1 containing
pointers to RLNZ
as output from subroutine LSCXD/DLSCXD. The nonzeros
in column J of
the factor are stored from location ILNZ(J) to ILNZ(J + 1) − 1. (Input)
The values (RLNZ, ILNZ, NZSUB, INZSUB) give the
off-diagonal nonzeros of the factor in a compressed subscript data format.
DIAGNL — Complex vector of length N containing the diagonals of the Cholesky factor as output from subroutine LNFZD/DLNFZD. (Input)
IPER — Vector of length N containing the
ordering as output from subroutine LSCXD/DLSCXD.
(Input)
IPER(I) = K indicates that the
original row K
is the new row I.
B — Complex vector of length N containing the right-hand side. (Input)
X — Complex vector of length N containing the solution. (Output)
FORTRAN 90 Interface
Generic: CALL LFSZD (N, MAXZUB, NZSUB, INZSUB, MAXNZ, RLNZ, ILNZ, DIAGNL, IPER, B, X)
Specific: The specific interface names are S_LFSZD and D_LFSZD.
FORTRAN 77 Interface
Single: CALL LFSZD (N, MAXSUB, NZSUB, INZSUB, MAXNZ, RLNZ, ILNZ, DIAGNL, IPER, B, X)
Double: The double precision name is DLFSZD.
Description
Consider the linear equation
Ax = b
where A is sparse, positive definite and Hermitian. The sparse coordinate format for the matrix A requires one complex and two integer vectors. The complex array a contains all the nonzeros in the lower triangle of A including the diagonal. Let the number of nonzeros be nz. The two integer arrays irow and jcol, each of length nz, contain the row and column indices for these entries in A. That is
Airow(i),icol(i) = a(i), i = 1, …, nz
irow(i) ≥ jcol(i) i = 1, …, nz
with all other entries in the lower triangle of A zero.
The routine LFSZD computes the solution of the linear system given its Cholesky factorization. The factorization is performed by calling LSCXD followed by LNFZD. The routine LSCXD computes a minimum degree ordering or uses a user-supplied ordering to set up the sparse data structure for the Cholesky factor, L. Then the routine LNFZD produces the numerical entries in L so that we have
P APT = LLH
Here P is the permutation matrix determined by the ordering.
The numerical computations can be carried out in one of two ways. The first method performs the factorization using a multifrontal technique. This option requires more storage but in certain cases will be faster. The multifrontal method is based on the routines in Liu (1987). For detailed description of this method, see Liu (1990), also Duff and Reid (1983, 1984), Ashcraft (1987), Ashcraft et al. (1987), and Liu (1986, 1989). The second method is fully described in George and Liu (1981). This is just the standard factorization method based on the sparse compressed storage scheme. Finally, the solution x is obtained by the following calculations:
1) Ly1 = Pb
2) LH y2 = y1
3) x = PT y2
Comments
Informational error
Type Code
4 1 The input matrix is numerically singular.
Example
As an example, consider the 3 × 3 linear system:
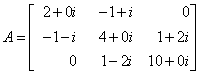
Let
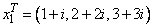
so that Ax1 = (−2 + 2i, 5 + 15i, 36 + 28i)T, and
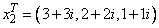
so that Ax2 = (2 + 6i, 7 − 5i, 16 + 8i)T. The number of nonzeros in the lower triangle of A is nz = 5. The sparse coordinate form for the lower triangle of A is given by:
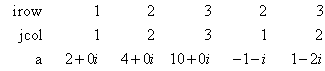
or equivalently by
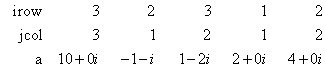
USE IMSL_LIBRARIES
INTEGER N, NZ, NRLNZ
PARAMETER (N=3, NZ=5, NRLNZ=5)
!
INTEGER IJOB, ILNZ(N+1), INVPER(N), INZSUB(N+1), IPER(N),&
IROW(NZ), ISPACE, JCOL(NZ), MAXNZ, MAXSUB,&
NZSUB(3*NZ)
COMPLEX A(NZ), B1(N), B2(N), DIAGNL(N), RLNZ(NRLNZ), X(N)
REAL RPARAM(2)
!
DATA A/(2.0,0.0), (4.0,0.0), (10.0,0.0), (-1.0,-1.0), (1.0,-2.0)/
DATA B1/(-2.0,2.0), (5.0,15.0), (36.0,28.0)/
DATA B2/(2.0,6.0), (7.0,5.0), (16.0,8.0)/
DATA IROW/1, 2, 3, 2, 3/
DATA JCOL/1, 2, 3, 1, 2/
! Select minimum degree ordering
! for multifrontal method
IJOB = 3
! Use default workspace
MAXSUB = 3*NZ
CALL LSCXD (IROW, JCOL, NZSUB,
INZSUB, MAXNZ, ILNZ, INVPER,
&
IJOB=IJOB, MAXSUB=MAXSUB, IPER=IPER,
ISPACE=ISPACE)
! Check if NRLNZ is large enough
IF (NRLNZ .GE. MAXNZ) THEN
! Choose multifrontal method
IJOB = 2
CALL LNFZD (A, IROW, JCOL, MAXSUB, NZSUB, INZSUB,&
MAXNZ, ILNZ, IPER, INVPER, ISPACE, DIAGNL,&
RLNZ, RPARAM, IJOB=IJOB)
! Solve A * X1 = B1
CALL LFSZD (N, MAXSUB, NZSUB, INZSUB, MAXNZ, RLNZ, ILNZ, DIAGNL,&
IPER, B1, X)
! Print X1
CALL WRCRN (' x1 ', X, 1, N,1)
! Solve A * X2 = B2
CALL LFSZD (N, MAXSUB, NZSUB, INZSUB, MAXNZ, RLNZ, ILNZ, DIAGNL,&
IPER, B2, X)
! Print X2
CALL WRCRN (' x2 ', X, 1, N,1)
END IF
!
END
Output
x1
1
2
3
( 1.000, 1.000) ( 2.000, 2.000) ( 3.000,
3.000)
x2
1 2 3
( 3.000, 3.000) ( 2.000, 2.000) ( 1.000, 1.000)
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |