Solves a complex sparse system of linear equations given the LU factorization of the coefficient matrix.
Required Arguments
NFAC — The number of nonzero coefficients in FACT as output from subroutine LFTZG/DLFTZG. (Input)
NL — The number of nonzero coefficients in the triangular matrix L excluding the diagonal elements as output from subroutine LFTZG/DLFTZG. (Input)
FACT — Complex vector of length NFAC containing the nonzero elements of L (excluding the diagonals) in the first NL locations and the nonzero elements of U in NL+ 1 to NFAC locations as output from subroutine LFTZG/DLFTZG. (Input)
IRFAC — Vector of length NFAC containing the row numbers of the corresponding elements in FACT as output from subroutine LFTZG/DLFTZG. (Input)
JCFAC — Vector of length NFAC containing the column numbers of the corresponding elements in FACT as output from subroutine LFTZG/DLFTZG. (Input)
IPVT — Vector of length N containing the row pivoting information for the LU factorization as output from subroutine LFTZG/DLFTZG. (Input)
JPVT — Vector of length N containing the column pivoting information for the LU factorization as output from subroutine LFTZG/DLFTZG. (Input)
B — Complex vector of length N containing the right-hand side of the linear system. (Input)
X — Complex vector of length N containing the solution to the linear system. (Output)
Optional Arguments
N — Number of equations.
(Input)
Default: N = size (B,1).
IPATH — Path indicator. (Input)
IPATH = 1
means the system Ax = b is solved.
IPATH = 2 means the
system AH
x = b is solved.
Default: IPATH = 1.
FORTRAN 90 Interface
Generic: CALL LFSZG (NFAC, NL, FACT, IRFAC, JCFAC, IPVT, JPVT, B, X [,…])
Specific: The specific interface names are S_LFSZG and D_LFSZG.
FORTRAN 77 Interface
Single: CALL LFSZG (N, NFAC, NL, FACT, IRFAC, JCFAC, IPVT, JPVT, B, IPATH, X)
Double: The double precision name is DLFSZG.
Description
Consider the linear equation
Ax = b
where A is a complex n × n sparse matrix. The sparse coordinate format for the matrix A requires one complex and two integer vectors. The complex array a contains all the nonzeros in A. Let the number of nonzeros be nz. The two integer arrays irow and jcol, each of length nz, contain the row and column numbers for these entries in A. That is
Airow(i),icol(i) = a(i), i = 1,… , nz
with all other entries in A zero.
The routine LFSZG computes the solution of the linear equation given its LU factorization. The factorization is performed by calling LFTZG. The solution of the linear system is then found by the forward and backward substitution. The algorithm can be expressed as
P AQ = LU
where P and Q are the row and column permutation matrices determined by the Markowitz strategy (Duff et al. 1986), and L and U are lower and upper triangular matrices, respectively.
Finally, the solution x is obtained by the following calculations:
1) Lz = Pb
2) Uy = z
3) x = Qy
For more details, see Crowe et al. (1990).
Example
As an example, consider the 6 × 6 linear system:

Let
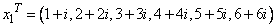
so that
Ax1 = (3 + 17i, −19 + 5i, 6 + 18i, −38 + 32i, −63 + 49i, −57 + 83i)T
and
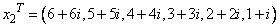
so that
Ax2 = (18 + 102i, −16 + 16i, 8 + 24i, −11 −11i, −63 + 7i, −132 + 106i)T
The sparse coordinate form for A is given by:

USE
LFSZG_INT
USE
WRCRN_INT
USE
LFTZG_INT
INTEGER N, NZ
PARAMETER (N=6, NZ=15)
!
INTEGER IPATH, IPVT(N), IRFAC(3*NZ), IROW(NZ),&
JCFAC(3*NZ), JCOL(NZ), JPVT(N), NFAC, NL
COMPLEX A(NZ), B(N,2), FACT(3*NZ), X(N)
CHARACTER TITLE(2)*2
!
DATA A/(3.0,7.0), (3.0,2.0), (-3.0,0.0), (-1.0,3.0), (4.0,2.0),&
(10.0,7.0), (-5.0,4.0), (1.0,6.0), (-1.0,12.0), (-5.0,0.0),&
(12.0,2.0), (-2.0,8.0), (-2.0,-4.0), (-1.0,2.0), (-7.0,7.0)/
DATA B/(3.0,17.0), (-19.0,5.0), (6.0,18.0), (-38.0,32.0),&
(-63.0,49.0), (-57.0,83.0), (18.0,102.0), (-16.0,16.0),&
(8.0,24.0), (-11.0,-11.0), (-63.0,7.0), (-132.0,106.0)/
DATA IROW/6, 2, 2, 4, 3, 1, 5, 4, 6, 5, 5, 6, 4, 2, 5/
DATA JCOL/6, 2, 3, 5, 3, 1, 1, 4, 1, 4, 5, 2, 1, 4, 6/
DATA TITLE/'x1','x2'/
!
NFAC = 3*NZ
! Perform LU factorization
CALL LFTZG (A, IROW, JCOL, NFAC, NL, FACT, IRFAC, JCFAC, IPVT, JPVT)
!
IPATH = 1
DO 10 I = 1,2
! Solve A * X(i) = B(i)
CALL LFSZG (NFAC, NL, FACT, IRFAC, JCFAC, IPVT, JPVT,&
B(:,I), X)
CALL WRCRN (TITLE(I), X)
10 CONTINUE
!
END
Output
x1
1 ( 1.000, 1.000)
2 ( 2.000, 2.000)
3 ( 3.000,
3.000)
4 ( 4.000, 4.000)
5 ( 5.000, 5.000)
6 ( 6.000,
6.000)
x2
1 ( 6.000, 6.000)
2 ( 5.000, 5.000)
3 ( 4.000, 4.000)
4 ( 3.000, 3.000)
5 ( 2.000, 2.000)
6 ( 1.000, 1.000)
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |