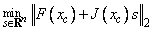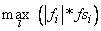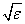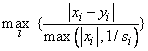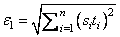NEQBF

Solves a system of nonlinear equations using factored secant update with a finite-difference approximation to the Jacobian .

Required Arguments

FCN — User-supplied SUBROUTINE to evaluate the system of equations to be solved. The usage is CALL FCN (N, X, F), where

N – Length of X and F. (Input)

X – The point at which the functions are evaluated. (Input)
X should not be changed by FCN.

F – The computed function values at the point X. (Output)

FCN must be declared EXTERNAL in the calling program.

X — Vector of length N containing the approximate solution. (Output)

Optional Arguments

N — Dimension of the problem. (Input)
Default: N = size (X,1).

XGUESS — Vector of length N containing initial guess of the root. (Input)
Default: XGUESS = 0.0.

XSCALE — Vector of length N containing the diagonal scaling matrix for the variables. (Input)
XSCALE is used mainly in scaling the distance between two points. In the absence of other information, set all entries to 1.0. If internal scaling is desired for XSCALE, set IPARAM (6) to 1.
Default: XSCALE = 1.0.

FSCALE — Vector of length N containing the diagonal scaling matrix for the functions. (Input)
FSCALE is used mainly in scaling the function residuals. In the absence of other information, set all entries to 1.0.
Default: FSCALE = 1.0.

IPARAM — Parameter vector of length 6. (Input/Output)
Set IPARAM (1) to zero for default values of IPARAM and RPARAM. See Comment 4 .
Default: IPARAM = 0.

RPARAM — Parameter vector of length 5. (Input/Output)
See Comment 4.

FVEC — Vector of length N containing the values of the functions at the approximate solution. (Output)

FORTRAN 90 Interface

Generic: CALL NEQBF (FCN, X [,…])

Specific: The specific interface names are S_NEQBF and D_NEQBF.

FORTRAN 77 Interface

Single: CALL NEQBF (FCN, N, XGUESS, XSCALE, FSCALE, IPARAM, RPARAM, X, FVEC)

Double: The double precision name is DNEQBF.

Description

Routine NEQBF uses a secant algorithm to solve a system of nonlinear equations, i.e.,

F(x) = 0

where F : R n ® R n, and x Î R n.

From a current point, the algorithm uses a double dogleg method to solve the following subproblem approximately:

subject to || s ||2 ≤ d c

to get a direction s c, where F(x c) and J(x c) are the function values and the approximate Jacobian respectively evaluated at the current point x c. Then, the function values at the point x n = x c + s c are evaluated and used to decide whether the new point x n should be accepted.

When the point x n is rejected, this routine reduces the trust region d c and goes back to solve the subproblem again. This procedure is repeated until a better point is found.

The algorithm terminates if the new point satisfies the stopping criterion. Otherwise, d c is adjusted, and the approximate Jacobian is updated by Broyden's formula,

where J n = J(x n), J c = J(x c), and y = F (x n) - F (x c). The algorithm then continues using the new point as the current point, i.e. x c ¬ x n.

For more details, see Dennis and Schnabel (1983, Chapter 8).

Since a finite-difference method is used to estimate the initial Jacobian, for single precision calculation, the Jacobian may be so incorrect that the algorithm terminates far from a root. In such cases, high precision arithmetic is recommended. Also, whenever the exact Jacobian can be easily provided, IMSL routine NEQBJ should be used instead.

Comments

1. Workspace may be explicitly provided, if desired, by use of N2QBF/DN2QBF. The reference is:

CALL N2QBF (FCN, N, XGUESS, XSCALE, FSCALE, IPARAM, RPARAM, X, FVEC, WK, LWK)

The additional arguments are as follows:

WK — A work vector of length LWK. On output WK contains the following information:

The third N locations contain the last step taken.

The fourth N locations contain the last Newton step.

The final N 2 locations contain an estimate of the Jacobian at the solution.

LWK — Length of WK, which must be at least 2 * N 2 + 11 * N. (Input)

2. Informational errors

Type Code

3 1 The last global step failed to decrease the 2-norm of F(X) sufficiently; either the current point is close to a root of F(X) and no more accuracy is possible, or the secant approximation to the Jacobian is inaccurate, or the step tolerance is too large.

3 3 The scaled distance between the last two steps is less than the step tolerance; the current point is probably an approximate root of F(X) (unless STEPTL is too large).

3 4 Maximum number of iterations exceeded.

3 5 Maximum number of function evaluations exceeded.

3 7 Five consecutive steps of length STEPMX have been taken; either the 2-norm of F(X) asymptotes from above to a finite value in some direction or the maximum allowable step size STEPMX is too small.

3. The stopping criterion for NEQBF occurs when the scaled norm of the functions is less than the scaled function tolerance (RPARAM(1)).

4. If the default parameters are desired for NEQBF, then set IPARAM(1) to zero and call routine NEQBF. Otherwise, if any nondefault parameters are desired for IPARAM or RPARAM, then the following steps should be taken before calling NEQBF:

CALL N4QBJ (IPARAM, RPARAM)
Set nondefault values for desired IPARAM, RPARAM elements.

Note that the call to N4QBJ will set IPARAM and RPARAM to their default values, so only nondefault values need to be set above.

The following is a list of the parameters and the default values:

IPARAM — Integer vector of length 6.

IPARAM(1) = Initialization flag.

IPARAM(2) = Number of good digits in the function.
Default: Machine dependent.

IPARAM(3) = Maximum number of iterations.
Default: 100.

IPARAM(4) = Maximum number of function evaluations.
Default: 400.

IPARAM(5) = Maximum number of Jacobian evaluations.
Default: not used in NEQBF.

IPARAM(6) = Internal variable scaling flag.
If IPARAM(6) = 1, then the values of XSCALE are set internally.
Default: 0.

RPARAM — Real vector of length 5.

RPARAM(1) = Scaled function tolerance.
The scaled norm of the functions is computed as

where f i is the i-th component of the function vector F, and fs i is the i-th component of FSCALE.
Default:

where ɛ is the machine precision.

RPARAM(2) = Scaled step tolerance. (STEPTL)
The scaled norm of the step between two points x and y is computed as

where s i is the i-th component of XSCALE.
Default: ɛ 2 /3, where ɛ is the machine precision.

RPARAM(3) = False convergence tolerance.
Default: not used in NEQBF.

RPARAM(4) = Maximum allowable step size. (STEPMX)

Default: 1000 * max(ɛ 1, ɛ 2), where

ɛ 2 = ||s|2, s = XSCALE, and t = XGUESS.

RPARAM(5) = Size of initial trust region.
Default: based on the initial scaled Cauchy step.

If double precision is desired, then DN4QBJ is called and RPARAM is declared double precision.

5. Users wishing to override the default print/stop attributes associated with error messages issued by this routine are referred to “Error Handling ” in the Introduction.

Example

The following 3 ´ 3 system of nonlinear equations:

is solved with the initial guess (4.0, 4.0, 4.0).

USE NEQBF_INT

USE UMACH_INT

IMPLICIT NONE

! Declare variables

INTEGER N

PARAMETER (N=3)

INTEGER K, NOUT

REAL X(N), XGUESS(N)

EXTERNAL FCN

! Set values of initial guess

! XGUESS = ( 4.0 4.0 4.0 )

DATA XGUESS/3*4.0/

! Find the solution

CALL NEQBF (FCN, X, XGUESS=XGUESS)

! Output

CALL UMACH (2, NOUT)

WRITE (NOUT,99999) (X(K),K=1,N)

99999 FORMAT (' The solution to the system is', /, ' X = (', 3F8.3, &

')')

END

! User-defined subroutine

SUBROUTINE FCN (N, X, F)

INTEGER N

REAL X(N), F(N)

REAL EXP, SIN

INTRINSIC EXP, SIN

F(1) = X(1) + EXP(X(1)-1.0) + (X(2)+X(3))*(X(2)+X(3)) - 27.0

F(2) = EXP(X(2)-2.0)/X(1) + X(3)*X(3) - 10.0

F(3) = X(3) + SIN(X(2)-2.0) + X(2)*X(2) - 7.0

RETURN

END

Output

The solution to the system is
X = ( 1.000 2.000 3.000)

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260