Computes the 1-norm of a real matrix.

Required Arguments

A — Real NRA by NCA matrix whose 1-norm is to be computed.   (Input)

ANORM — Real scalar containing the 1-norm of A.   (Output)

Optional Arguments

NRA — Number of rows of A.   (Input)
Default: NRA = size (A,1).

NCA — Number of columns of A.   (Input)
Default: NCA = size (A,2).

LDA — Leading dimension of A exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDA = size (A,1).

FORTRAN 90 Interface

Generic:          CALL NR1RR (A, ANORM [,…])

Specific:          The specific interface names are S_NR1RR and D_NR1RR.

FORTRAN 77 Interface

Single:            CALL NR1RR (NRA, NCA, A, LDA, ANORM)

Double:          The double precision name is DNR1RR.

Description

The routine NR1RR computes the 1-norm of a real rectangular matrix A. If m = NRA and n = NCA, then the 1-norm of A is

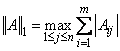
This is the maximum of the sums of the absolute values of the column elements.

Example

Compute the 1-norm of a 3 ´ 4 real rectangular matrix.

 

      USE NR1RR_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                             Declare variables

      INTEGER    NCA, NRA

      PARAMETER  (NCA=4, NRA=3)

!

      INTEGER    NOUT

      REAL       A(NRA,NCA), ANORM

!

!                 Set values for A

!                         A = ( 1.0  0.0  2.0  0.0 )

!                             ( 3.0  4.0 -1.0  0.0 )

!                             ( 2.0  1.0  2.0  1.0 )

!

      DATA A/1.0, 3.0, 2.0, 0.0, 4.0, 1.0, 2.0, -1.0, 2.0, 0.0, 0.0, &

          1.0/

!                                 Compute the L1 norm of A

      CALL NR1RR (A, ANORM)

!                                 Print results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,*) ' The 1-norm of A is ', ANORM

      END

Output

 

The 1-norm of A is     6.00000

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260