Computes a rational weighted Chebyshev approximation to a continuous function on an interval.
Required Arguments
F — User-supplied FUNCTION to be approximated. The form is F(X), where
X – Independent
variable. (Input)
F – The function value.
(Output)
F must be declared EXTERNAL in the calling program.
PHI — User-supplied FUNCTION to supply the variable transformation which must be continuous and monotonic. The form is PHI(X), where
X – Independent variable. (Input)
PHI – The function value. (Output)
PHI must be declared EXTERNAL in the calling program.
WEIGHT — User-supplied FUNCTION to scale the maximum error. It must be continuous and nonvanishing on the closed interval (A, B). The form is WEIGHT(X), where
X –
Independent variable. (Input)
WEIGHT – The function value.
(Output)
WEIGHT must be declared EXTERNAL in the calling program.
A — Lower end of the interval on which the approximation is desired. (Input)
B — Upper end of the interval on which the approximation is desired. (Input)
P — Vector of length N + 1 containing the coefficients of the numerator polynomial. (Output)
Q — Vector of length M + 1 containing the coefficients of the denominator polynomial. (Output)
ERROR — Min-max error of approximation. (Output)
Optional Arguments
N — The degree of
the numerator. (Input)
Default: N = size (P,1) – 1.
M — The degree of
the denominator. (Input)
Default: M = size (Q,1) – 1.
FORTRAN 90 Interface
Generic: CALL RATCH (F, PHI, WEIGHT, A, B, P, Q, ERROR [,…])
Specific: The specific interface names are S_RATCH and D_RATCH.
FORTRAN 77 Interface
Single: CALL RATCH (F, PHI, WEIGHT, A, B, N, M, P, Q, ERROR)
Double: The double precision name is DRATCH.
Description
The routine RATCH is designed to compute the best weighted L∞ (Chebyshev) approximant to a given function. Specifically, given a weight function w = WEIGHT, a monotone function ɸ = PHI, and a function f to be approximated on the interval [a, b], the subroutine RATCH returns the coefficients (in P and Q) for a rational approximation to f on [a, b]. The user must supply the degree of the numerator N and the degree of the denominator M of the rational function
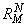
The goal is to produce coefficients which minimize the expression
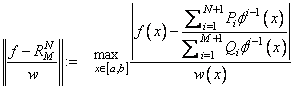
Notice that setting ɸ(x) = x yields ordinary rational approximation. A typical use of the function ɸ occurs when one wants to approximate an even function on a symmetric interval, say [−a, a] using ordinary rational functions. In this case, it is known that the answer must be an even function. Hence, one can set ɸ(x) = x2, only approximate on [0, a], and decrease by one half the degrees in the numerator and denominator.
The algorithm implemented in this subroutine is designed for fast execution. It assumes that the best approximant has precisely N + M + 2 equi-oscillations. That is, that there exist N + M + 2 points t1 < … < tN+M+2 satisfying
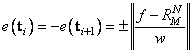
Such points are called alternants. Unfortunately, there are many instances in which the best rational approximant to the given function has either fewer alternants or more alternants. In this case, it is not expected that this subroutine will perform well. For more information on rational Chebyshev approximation, the reader can consult Cheney (1966). The subroutine is based on work of Cody, Fraser, and Hart (1968).
Comments
1. Workspace may be explicitly provided, if desired, by use of R2TCH/DR2TCH. The reference is:
CALL R2TCH (F, PHI, WEIGHT, A, B, N, M, P, Q, ERROR, ITMAX, IWK, WK)
The additional arguments are as follows:
ITMAX —
Maximum number of iterations. (Input)
The default value is
20.
IWK — Workspace vector of length (N + M + 2). (Workspace)
WK — Workspace vector of length (N + M + 8) * (N + M + 2). (Workspace)
2. Informational errors
Type Code
3 1 The maximum number of iterations has been reached. The routine R2TCH may be called directly to set a larger value for ITMAX.
3 2 The error was reduced as far as numerically possible. A good approximation is returned in P and Q, but this does not necessarily give the Chebyshev approximation.
4 3 The linear system that defines P and Q was found to be algorithmically singular. This indicates the possibility of a degenerate approximation.
4 4 A sequence of critical points that was not monotonic generated. This indicates the possibility of a degenerate approximation.
4 5 The value of the error curve at some critical point is too large. This indicates the possibility of poles in the rational function.
4 6 The weight function cannot be zero on the closed interval (A, B).
Example
In this example, we compute the best rational approximation to the gamma function, Γ, on the interval [2, 3] with weight function w = 1 and N = M = 2. We display the maximum error and the coefficients. This problem is taken from the paper of Cody, Fraser, and Hart (1968). We compute in double precision due to the conditioning of this problem.
USE RATCH_INT
USE UMACH_INT
IMPLICIT NONE
INTEGER M, N
PARAMETER (M=2, N=2)
!
INTEGER NOUT
DOUBLE PRECISION A, B, ERROR, F, P(N+1), PHI, Q(M+1), WEIGHT
EXTERNAL F, PHI, WEIGHT
!
A = 2.0D0
B = 3.0D0
! Compute double precision rational
! approximation
CALL RATCH (F, PHI, WEIGHT, A, B, P, Q, ERROR)
! Get output unit number
CALL UMACH (2, NOUT)
! Print P, Q and min-max error
WRITE (NOUT,'(1X,A)') 'In double precision we have:'
WRITE (NOUT,99999) 'P = ', P
WRITE (NOUT,99999) 'Q = ', Q
WRITE (NOUT,99999) 'ERROR = ', ERROR
99999 FORMAT (' ', A, 5X, 3F20.12, /)
END
! -----------------------------------------------------------------------
!
DOUBLE PRECISION FUNCTION F (X)
DOUBLE PRECISION X
!
DOUBLE PRECISION DGAMMA
EXTERNAL DGAMMA
!
F = DGAMMA(X)
RETURN
END
! -----------------------------------------------------------------------
!
DOUBLE PRECISION FUNCTION PHI (X)
DOUBLE PRECISION X
!
PHI = X
RETURN
END
! -----------------------------------------------------------------------
!
DOUBLE PRECISION FUNCTION WEIGHT (X)
DOUBLE PRECISION X
!
DOUBLE PRECISION DGAMMA
EXTERNAL DGAMMA
!
WEIGHT = DGAMMA(X)
RETURN
END
Output
In double precision we
have:
P
=
1.265583562487
-0.650585004466
0.197868699191
Q
=
1.000000000000 -0.064342721236
-0.028851461855
ERROR
=
-0.000026934190
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |