Computes recurrence coefficients for various monic polynomials.

Required Arguments

N — Number of recurrence coefficients.   (Input)

B — Array of length N containing recurrence coefficients.   (Output)

C — Array of length N containing recurrence coefficients.   (Output)

Optional Arguments

IWEIGH — Index of the weight function.   (Input)
Default: IWEIGH = 1.

           

ALPHA — Parameter used in the weight function with some values of IWEIGH, otherwise it is ignored.   (Input)
Default: ALPHA=1.0.

BETAW — Parameter used in the weight function with some values of IWEIGH, otherwise it is ignored.   (Input)
Default: BETAW=1.0.

FORTRAN 90 Interface

Generic:          CALL RECCF (N, B, C [,…])

Specific:         The specific interface names are S_RECCF and D_RECCF.

FORTRAN 77 Interface

Single:     CALL RECCF (N, IWEIGH, ALPHA, BETAW, B, C)

Double:          The double precision name is DRECCF.

Description

The routine RECCF produces the recurrence coefficients for the orthogonal polynomials for some of the most important weights. It is assumed that the orthogonal polynomials are monic; hence, the three-term recursion may be written as

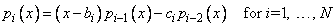
where p0 = 1 and p-1 = 0. It is obvious from this representation that the degree of pi is i and that pi is monic. In order for the recurrence to give rise to a sequence of orthogonal polynomials (with respect to a nonnegative measure), it is necessary and sufficient that ci > 0.

Comments

The recurrence coefficients B(I) and C(I) define the monic polynomials via the relation
P(I) = (X − B(I + 1)) * P(I − 1) − C(I + 1) * P(I − 2). The zero-th moment

 

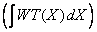
of the weight function is returned in C(1).

Example

Here, we obtain the well-known recurrence relations for the first six monic Legendre polynomials, Chebyshev polynomials of the first kind, and Laguerre polynomials.

 

      USE RECCF_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

      INTEGER    N

      PARAMETER (N=6)

      INTEGER    I, IWEIGH, NOUT

      REAL       ALPHA, B(N), C(N), BETAW

!                                 Get output unit number

      CALL UMACH (2, NOUT)

!

      CALL RECCF (N, B, C)

      WRITE (NOUT,99996)

      WRITE (NOUT,99999) (I,B(I),I,C(I),I=1,N)

!

      IWEIGH = 2

      CALL RECCF (N, B, C, IWEIGH=IWEIGH)

      WRITE (NOUT,99997)

      WRITE (NOUT,99999) (I,B(I),I,C(I),I=1,N)

!

      IWEIGH = 6

      ALPHA = 0.0

      BETAW  = 0.0

      CALL RECCF (N, B, C, IWEIGH=IWEIGH, ALPHA=ALPHA)

      WRITE (NOUT,99998)

      WRITE (NOUT,99999) (I,B(I),I,C(I),I=1,N)

!

99996 FORMAT (1X, 'Legendre')

99997 FORMAT (/, 1X, 'Chebyshev, first kind')

99998 FORMAT (/, 1X, 'Laguerre')

99999 FORMAT (6(6X,'B(',I1,') = ',F8.4,7X,'C(',I1,') = ',F8.5,/))

      END

Output

 

Legendre
B(1) =   0.0000       C(1) =  2.00000
B(2) =   0.0000       C(2) =  0.33333
B(3) =   0.0000       C(3) =  0.26667
B(4) =   0.0000       C(4) =  0.25714
B(5) =   0.0000       C(5) =  0.25397
B(6) =   0.0000       C(6) =  0.25253

Chebyshev, first kind
B(1) =   0.0000       C(1) =  3.14159
B(2) =   0.0000       C(2) =  0.50000
B(3) =   0.0000       C(3) =  0.25000
B(4) =   0.0000       C(4) =  0.25000
B(5) =   0.0000       C(5) =  0.25000
B(6) =   0.0000       C(6) =  0.25000

Laguerre
B(1) =   1.0000       C(1) =  1.00000
B(2) =   3.0000       C(2) =  1.00000
B(3) =   5.0000       C(3) =  4.00000
B(4) =   7.0000       C(4) =  9.00000
B(5) =   9.0000       C(5) = 16.00000
B(6) =  11.0000       C(6) = 25.00000

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260