This routine writes the matrix data to a file.  The data is transmitted from the two-dimensional block-cyclic form used by ScaLAPACK routines.  This routine contains a call to a barrier routine so that if one process is writing the file and an alternate process is to read it, the results will be synchronized. All processors in the BLACS context call the routine.

Required Arguments

File_Name —  A character variable naming the file to receive the matrix data. (Input)
This file is opened with “STATUS=”UNKNOWN.”  If any access violation happens, a type = terminal error message will occur.  If the file already exists it will be overwritten.  After the contents are written, the file is closed. This file is written with a loop logically equivalent to groups of writes:

WRITE() ((BUFFER(I,J), I=1,M), J=1, NB)
or (optionally):

WRITE() ((BUFFER(I,J), J=1,N), I=1, MB)

DESC_A(*) — The nine integer parameters associated with the ScaLAPACK matrix descriptor. Values for NB, MB, LDA are contained in this array. (Input)

A(LDA,*) — This is an assumed-size array, with leading dimension LDA, containing this processor's piece of the block-cyclic matrix.  The data type for A(*,*) is any of five Fortran intrinsic types: integer; single precision, real; double precision, real; single precision, complex; or double precision, complex. (Input)

Optional Arguments

Format —A character variable containing a format to be used for writing the file that receives matrix data.  If this argument is not present, an unformatted or list-directed write is used. (Input)

iopt — Derived type array with the same precision as the array A(*,*), used for passing optional data to ScaLAPACK_WRITE. Use single precision when A(*,*) is type INTEGER.  (Input)
The options are as follows:

Packaged Options for ScaLAPACK_WRITE
Option Prefix = ?	Option Name	Option Value
S_, d_	ScaLAPACK_WRITE_UNIT	1
S_, d_	ScaLAPACK_WRITE_FROM_PROCESS	2
S_, d_	ScaLAPACK_WRITE_BY_ROWS	3

 

iopt(IO) =ScaLAPACK_WRITE_UNIT
Sets the unit number to the integer component of
iopt(IO + 1)%idummy.  The default unit number is the value 11.

iopt(IO) = ScaLAPACK_WRITE_FROM_PROCESS
Sets the process number that writes the named file to the integer component of iopt(IO + 1)%idummy.  The default process number is the value 0.

iopt(IO) = ScaLAPACK_WRITE_BY_ROWS
Write the matrix by rows to the named file.  By default the matrix is written by columns.

FORTRAN 90 Interface

Generic:        CALL ScaLAPACK_WRITE (File_Name, DESC_A, A [,…])

Specific:       The specific interface names are S_ScaLAPACK_WRITE and
                                D_ScaLAPACK_WRITE.

Description

Subroutine ScaLAPACK_WRITE writes columns or rows of a problem matrix output by a ScaLAPACK routine.  It uses the two-dimensional block-cyclic array descriptor for the matrix to extract the data from the assumed-size arrays on the processors.  The blocks of data are transmitted and received, then written.  The block sizes, contained in the array descriptor, determines the data set size for each blocking send and receive pair. The number of these synchronization points is proportional to 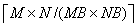.  A temporary local buffer is allocated for staging the matrix data.  It is of size M by NB, when writing by columns, or N by MB, when writing by rows.

Example 1:  Distributed Transpose of a Matrix, In Place

The program SCPK_EX1 illustrates an in-situ transposition of a matrix.  An 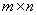matrix, 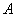, is written to a file, by rows.  The 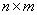matrix, 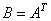, overwrites storage for 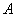.  Two temporary files are created and deleted.  This algorithm for transposing a matrix is not efficient.  It is used to illustrate the read and write routines and optional arguments for writing of data by matrix rows.

 

  program scpk_ex1

! This is Example 1 for ScaLAPACK_READ and ScaLAPACK_WRITE.

! It shows in-situ or in-place transposition of a

! block-cyclic matrix.

USE ScaLAPACK_SUPPORT

USE ERROR_OPTION_PACKET

USE MPI_SETUP_INT

 

IMPLICIT NONE

INCLUDE "mpif.h"

 

INTEGER, PARAMETER :: M=6, N=6, NIN=10

INTEGER  DESC_A(9), IERROR, INFO, I, J, K, L, MXLDA, MXCOL

LOGICAL :: GRID1D = .TRUE., NSQUARE = .TRUE.

real(kind(1d0)), allocatable :: A(:,:), A0(:,:)

real(kind(1d0)) ERROR

TYPE(d_OPTIONS) IOPT(1)

 

    MP_NPROCS=MP_SETUP()

 

!  Set up a 1D processor grid and define its context ID, MP_ICTXT

   CALL SCALAPACK_SETUP(M, N, NSQUARE, GRID1D)

!  Get the array descriptor entities MXLDA, and MXCOL

   CALL SCALAPACK_GETDIM(M, N, MP_MB, MP_NB, MXLDA, MXCOL)

!  Set up the array descriptor

   CALL DESCINIT(DESC_A, M, N, MP_MB, MP_NB, 0, 0, MP_ICTXT, &

   MXLDA, INFO)

!   Allocate space for local arrays

    ALLOCATE(A0(MXLDA,MXCOL))

 

! A root process is used to create the matrix data for the test.

IF(MP_RANK == 0) THEN

  ALLOCATE(A(M,N))

! Fill array with a pattern that is easy to recognize.

  K=0

  DO

   K=K+1; IF(10**K > N) EXIT

  END DO

  DO J=1,N

    DO I=1,M

! The values will appear, as decimals I.J, where I is

! the row and J is the column.

      A(I,J)=REAL(I)+REAL(J)*10d0**(-K)

    END DO

  END DO

 

  OPEN(UNIT=NIN, FILE='test.dat', STATUS='UNKNOWN')

! Write the data by columns.

  DO J=1,N,MP_NB

    WRITE(NIN,*) ((A(I,L),I=1,M),L=J,min(N,J+MP_NB-1))

  END DO

  CLOSE(NIN)

  DEALLOCATE(A)

  ALLOCATE(A(N,M))

END IF

 

! Read the matrix into the local arrays.

CALL ScaLAPACK_READ('test.dat', DESC_A, A0)

 

! To transpose, write the matrix by rows as the first step.

! This requires an option since the default is to write

! by columns.

IOPT(1)=ScaLAPACK_WRITE_BY_ROWS

CALL ScaLAPACK_WRITE("TEST.DAT", DESC_A, A0, IOPT=IOPT)

 

!  Resize the local storage

   DEALLOCATE(A0)

  CALL SCALAPACK_GETDIM(N, M, MP_NB, MP_MB, MXLDA, MXCOL)

!  Set up the array descriptor

!  Reshape the descriptor for the transpose of the matrix.

!  The number of rows and columns are swapped.

  CALL DESCINIT(DESC_A, N, M, MP_NB, MP_MB, 0, 0, MP_ICTXT, &

  MXLDA, INFO)

 

   ALLOCATE(A0(MXLDA,MXCOL))

 

!  Read the transpose matrix

 

CALL ScaLAPACK_READ("TEST.DAT", DESC_A, A0)

 

IF(MP_RANK == 0) THEN

 

! Open the used files and delete when closed.

  OPEN(UNIT=NIN, FILE='test.dat', STATUS='OLD')

  CLOSE(NIN,STATUS='DELETE')

  OPEN(UNIT=NIN, FILE='TEST.DAT', STATUS='OLD')

  DO J=1,M,MP_MB

    READ(NIN,*) ((A(I,L), I=1,N),L=J,min(M,J+MP_MB-1))

  END DO

  CLOSE(NIN,STATUS='DELETE')

  DO I=1,N

    DO J=1,M

! The values will appear, as decimals I.J, where I is the row

!  and J is the column.

      A(I,J)=REAL(J)+REAL(I)*10d0**(-K) - A(I,J)

    END DO

  END DO

  ERROR=SUM(ABS(A))

 END IF

 

! See to any error messages.

  call e1pop("Mp_setup")

 

! Check results on just one process.

IF(ERROR <= SQRT(EPSILON(ERROR)) .and. &

  MP_RANK == 0) THEN

  write(*,*) " Example 1 for BLACS is correct."

END IF

 

! Deallocate storage arrays and exit from BLACS.

IF(ALLOCATED(A)) DEALLOCATE(A)

IF(ALLOCATED(A0)) DEALLOCATE(A0)

 

! Exit from using this process grid.

  CALL SCALAPACK_EXIT( MP_ICTXT )

! Shut down MPI

  MP_NPROCS = MP_SETUP(‘FINAL')

END

Output

 

Example 1 for BLACS is correct.

Additional Examples

Example 2:  Distributed Matrix Product with PBLAS

The program SCPK_EX2 illustrates computation of the matrix product 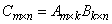.  The matrices on the right-hand side are random.  Three temporary files are created and deleted.  BLACS and PBLAS are used.  The problem size is such that the results are checked on one process.

  program scpk_ex2

! This is Example 2 for ScaLAPACK_READ and ScaLAPACK_WRITE.

! The product of two matrices is computed with PBLAS

! and checked for correctness.

 

USE ScaLAPACK_SUPPORT

USE MPI_SETUP_INT

 

IMPLICIT NONE

INCLUDE "mpif.h"

 

INTEGER, PARAMETER :: K=32, M=33, N=34, NIN=10

INTEGER INFO, IA, JA, IB, JB, IC, JC, MXLDA, MXCOL, MXLDB, &
  MXCOLB, MXLDC, MXCOLC, IERROR, I, J, L,&

  DESC_A(9), DESC_B(9), DESC_C(9)

LOGICAL :: GRID1D = .TRUE., NSQUARE = .TRUE.

 

 real(kind(1d0)) :: ALPHA, BETA, ERROR=1d0, SIZE_C

 real(kind(1d0)), allocatable, dimension(:,:) :: A,B,C,X(:),&

 A0, B0, C0

 

 MP_NPROCS=MP_SETUP()

 

! Set up a 1D processor grid and define its context ID, MP_ICTXT

  CALL SCALAPACK_SETUP(M, N, NSQUARE, GRID1D)

! Get the array descriptor entities

  CALL SCALAPACK_GETDIM(M, K, MP_MB, MP_NB, MXLDA, MXCOL)

  CALL SCALAPACK_GETDIM(K, N, MP_NB, MP_MB, MXLDB, MXCOLB)

  CALL SCALAPACK_GETDIM(M, N, MP_MB, MP_NB, MXLDC, MXCOLC)

! Set up the array descriptors

  CALL DESCINIT(DESC_A, M, K, MP_MB, MP_NB, 0, 0, MP_ICTXT, &

  MXLDA, INFO)

  CALL DESCINIT(DESC_B, K, N, MP_NB, MP_NB, 0, 0, MP_ICTXT, &

  MXLDB, INFO)

  CALL DESCINIT(DESC_C, M, N, MP_MB, MP_NB, 0, 0, MP_ICTXT, &

  MXLDC, INFO)

 

ALLOCATE(A0(MXLDA,MXCOL), B0(MXLDB,MXCOLB),C0(MXLDC,MXCOLC))

 

! A root process is used to create the matrix data for the test.

IF(MP_RANK == 0) THEN

  ALLOCATE(A(M,K), B(K,N), C(M,N), X(M))

  CALL RANDOM_NUMBER(A); CALL RANDOM_NUMBER(B)

 

  OPEN(UNIT=NIN, FILE='Atest.dat', STATUS='UNKNOWN')

! Write the data by columns.

  DO J=1,K,MP_NB

    WRITE(NIN,*) ((A(I,L),I=1,M),L=J,min(K,J+MP_NB-1))

  END DO

  CLOSE(NIN)

 

  OPEN(UNIT=NIN, FILE='Btest.dat', STATUS='UNKNOWN')

! Write the data by columns.

  DO J=1,N,MP_NB

    WRITE(NIN,*) ((B(I,L),I=1,K),L=J,min(N,J+MP_NB-1))

  END DO

  CLOSE(NIN)

END IF

 

! Read the factors into the local arrays.

CALL ScaLAPACK_READ('Atest.dat', DESC_A, A0)

CALL ScaLAPACK_READ('Btest.dat', DESC_B, B0)

 

! Compute the distributed product C = A x B.

ALPHA=1d0; BETA=0d0

IA=1; JA=1; IB=1; JB=1; IC=1; JC=1

C0=0

CALL pdGEMM &

  ("No", "No", M, N, K, ALPHA, A0, IA, JA,&

  DESC_A, B0, IB, JB, DESC_B, BETA,&

  C0, IC, JC, DESC_C )

 

! Put the product back on the root node.

Call ScaLAPACK_WRITE('Ctest.dat', DESC_C, C0)

 

IF(MP_RANK == 0) THEN

 

! Read the residuals and check them for size.

  OPEN(UNIT=NIN, FILE='Ctest.dat', STATUS='OLD')

 

! Read the data by columns.

  DO J=1,N,MP_NB

    READ(NIN,*) ((C(I,L),I=1,M),L=J,min(N,J+MP_NB-1))

  END DO

 

  CLOSE(NIN,STATUS='DELETE')

  SIZE_C=SUM(ABS(C)); C=C-matmul(A,B)

  ERROR=SUM(ABS(C))/SIZE_C

 

! Open other temporary files and delete them.

  OPEN(UNIT=NIN, FILE='Atest.dat', STATUS='OLD')

  CLOSE(NIN,STATUS='DELETE')

  OPEN(UNIT=NIN, FILE='Btest.dat', STATUS='OLD')

  CLOSE(NIN,STATUS='DELETE')

   

END IF

 

! See to any error messages.

call e1pop("Mp_Setup")

! Deallocate storage arrays and exit from BLACS.

IF(ALLOCATED(A)) DEALLOCATE(A)

IF(ALLOCATED(B)) DEALLOCATE(B)

IF(ALLOCATED(C)) DEALLOCATE(C)

IF(ALLOCATED(X)) DEALLOCATE(X)

IF(ALLOCATED(A0)) DEALLOCATE(A0)

IF(ALLOCATED(B0)) DEALLOCATE(B0)

IF(ALLOCATED(C0)) DEALLOCATE(C0)

 

! Check the results.

IF(ERROR <= SQRT(EPSILON(ALPHA)) .and. &

  MP_RANK == 0) THEN

  write(*,*) " Example 2 for BLACS and PBLAS is correct."

END IF

 

   ! Exit from using this process grid.

     CALL SCALAPACK_EXIT( MP_ICTXT )

  ! Shut down MPI

  MP_NPROCS = MP_SETUP(‘FINAL')

END

Output

 

Example 2 for BLACS and PBLAS is correct.

Example 3:  Distributed Linear Solver with ScaLAPACK

The program SCPK_EX3 illustrates solving a system of linear-algebraic equations, 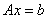by calling a ScaLAPACK routine directly.  The right-hand side is produced by defining 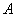 and 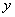 to have random values.  Then the matrix-vector product  is computed.  The problem size is such that the residuals,  are checked on one process.  Three temporary files are created and deleted. BLACS are used to define the process grid and provide further information identifying each process.  Then a ScaLAPACK routine is called directly to compute the approximate solution, .

 

  program scpk_ex3

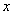! This is Example 3 for ScaLAPACK_READ and ScaLAPACK_WRITE.

! A linear system is solved with ScaLAPACK and checked.

USE ScaLAPACK_SUPPORT

USE ERROR_OPTION_PACKET

USE MPI_SETUP_INT

 

IMPLICIT NONE

 

INCLUDE "mpif.h"

INTEGER, PARAMETER :: N=9, NIN=10

INTEGER  INFO, IA, JA, IB, JB, MXLDA,MXCOL,&

  IERROR, I, J, L, DESC_A(9),&

  DESC_B(9), BUFF(3), RBUF(3)

 

LOGICAL :: COMMUTE = .TRUE., NSQUARE = .TRUE., GRID1D = .TRUE.

INTEGER, ALLOCATABLE :: IPIV0(:) 

real(kind(1d0)) :: ERROR=0d0, SIZE_Y

real(kind(1d0)), allocatable, dimension(:,:) :: A, B(:), &

  X(:), Y(:), A0, B0

 

  MP_NPROCS=MP_SETUP()

 

! Set up a 1D processor grid and define its context ID, MP_ICTXT

  CALL SCALAPACK_SETUP(N, N, NSQUARE, GRID1D)

! Get the array descriptor entities

  CALL SCALAPACK_GETDIM(N, N, MP_MB, MP_NB, MXLDA, MXCOL)

! Set up the array descriptors

  CALL DESCINIT(DESC_A, N, N, MP_MB, MP_NB, 0, 0, MP_ICTXT, &

  MXLDA, INFO)

  CALL DESCINIT(DESC_B, N, 1, MP_MB, MP_NB, 0, 0, MP_ICTXT, &

  MXLDA, INFO)

 

! Allocate local space for each array.

  ALLOCATE(A0(MXLDA,MXCOL), B0(MXLDA,1), IPIV0(MXLDA+MP_MB))

 

! A root process is used to create the matrix data for the test.

IF(MP_RANK == 0) THEN

  ALLOCATE(A(N,N), B(N), X(N), Y(N))

  CALL RANDOM_NUMBER(A); CALL RANDOM_NUMBER(Y)

 

! Compute the correct result.

  B=MATMUL(A,Y); SIZE_Y=SUM(ABS(Y))

  OPEN(UNIT=NIN, FILE='Atest.dat', STATUS='UNKNOWN')

 

! Write the data by columns.

  DO J=1,N,MP_NB

    WRITE(NIN,*) ((A(I,L),I=1,N),L=J,min(N,J+MP_NB-1))

  END DO

  CLOSE(NIN)

 

  OPEN(UNIT=NIN, FILE='Btest.dat', STATUS='UNKNOWN')

! Write the data by columns.

  WRITE(NIN,*) (B(I),I=1,N)

  CLOSE(NIN)

END IF

 

! Read the factors into the local arrays.

CALL ScaLAPACK_READ('Atest.dat', DESC_A, A0)

CALL ScaLAPACK_READ('Btest.dat', DESC_B, B0)

 

! Compute the distributed product solution to A x = b.

IA=1; JA=1; IB=1; JB=1

 

CALL pdGESV  (N, 1, A0, IA, JA, DESC_A, IPIV0, &

B0, IB, JB, DESC_B, INFO)

 

! Put the result on the root node.

Call ScaLAPACK_WRITE('Xtest.dat', DESC_B, B0)

 

IF(MP_RANK == 0) THEN

 

! Read the residuals and check them for size.

  OPEN(UNIT=NIN, FILE='Xtest.dat', STATUS='OLD')

 

! Read the approximate solution data.

      READ(NIN,*) X

      B=X-Y

 

  CLOSE(NIN,STATUS='DELETE')

  ERROR=SUM(ABS(B))/SIZE_Y

 

! Delete temporary files.

  OPEN(UNIT=NIN, FILE='Atest.dat', STATUS='OLD')

  CLOSE(NIN,STATUS='DELETE')

  OPEN(UNIT=NIN, FILE='Btest.dat', STATUS='OLD')

  CLOSE(NIN,STATUS='DELETE')

   

END IF

 

 

! See to any error messages.

call e1pop("Mp_Setup")

 

! Deallocate storage arrays

IF(ALLOCATED(A)) DEALLOCATE(A)

IF(ALLOCATED(B)) DEALLOCATE(B)

IF(ALLOCATED(X)) DEALLOCATE(X)

IF(ALLOCATED(Y)) DEALLOCATE(Y)

IF(ALLOCATED(A0)) DEALLOCATE(A0)

IF(ALLOCATED(B0)) DEALLOCATE(B0)

IF(ALLOCATED(IPIV0)) DEALLOCATE(IPIV0)

 

IF(ERROR <= SQRT(EPSILON(ERROR)) .and. MP_RANK == 0) THEN

  write(*,*) &

  " Example 3 for BLACS and ScaLAPACK solver is correct."

END IF

 

 ! Exit from using this process grid.

  CALL SCALAPACK_EXIT( MP_ICTXT )
! Shut down MPI

  MP_NPROCS = MP_SETUP(‘FINAL')

END

Output

 

Example 3 for BLACS and ScaLAPACK is correct.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260