Minimizes a function of N variables using a modified Newton method and a finite-difference Hessian.
Required Arguments
FCN User-supplied subroutine to evaluate the function to be minimized. The usage is CALL FCN (N, X, F), where
N Length of X. (Input)
X Vector of length N
at which point the function is evaluated. (Input)
X should not be
changed by FCN.
F The computed function value at the point X. (Output)
FCN must be declared EXTERNAL in the calling program.
GRAD
User-supplied subroutine to compute the gradient at the point X. The usage is
CALL GRAD
(N, X,
G), where
N Length of X and G. (Input)
X The point at which
the gradient is evaluated. (Input)
X should not be
changed by GRAD.
G The gradient evaluated at the point X. (Output)
GRAD must be declared EXTERNAL in the calling program.
X Vector of length N containing the computed solution. (Output)
Optional Arguments
N Dimension of
the problem. (Input)
Default: N = size
(X,1).
XGUESS Vector
of length N
containing initial guess. (Input)
Default: XGUESS = 0.0.
XSCALE Vector
of length N
containing the diagonal scaling matrix for the variables. (Input)
XSCALE is
used mainly in scaling the gradient and the distance between two points. In the
absence of other information, set all entries to 1.0.
Default: XSCALE = 1.0.
FSCALE Scalar
containing the function scaling. (Input)
FSCALE is used mainly
in scaling the gradient. In the absence of other information, set FSCALE to
1.0.
Default: FSCALE = 1.0.
IPARAM
Parameter vector of length 7. (Input/Output)
Set IPARAM(1) to zero for
default values of IPARAM and RPARAM. See
Comment 4.
Default: IPARAM = 0.
RPARAM
Parameter vector of length 7. (Input/Output)
See Comment 4.
FVALUE Scalar containing the value of the function at the computed solution. (Output)
FORTRAN 90 Interface
Generic: CALL UMIDH (FCN, GRAD, X [, ])
Specific: The specific interface names are S_UMIDH and D_UMIDH.
FORTRAN 77 Interface
Single: CALL UMIDH (FCN, GRAD, N, XGUESS, XSCALE, FSCALE, IPARAM, RPARAM, X, FVALUE)
Double: The double precision name is DUMIDH.
Description
The routine UMIDH uses a modified Newton method to find the minimum of a function f (x) of n variables. First derivatives must be provided by the user. The algorithm computes an optimal locally constrained step (Gay 1981) with a trust region restriction on the step. It handles the case that the Hessian is indefinite and provides a way to deal with negative curvature. For more details, see Dennis and Schnabel (1983, Appendix A) and Gay (1983).
Since a finite-difference method is used to estimate the Hessian for some single precision calculations, an inaccurate estimate of the Hessian may cause the algorithm to terminate at a noncritical point. In such cases, high precision arithmetic is recommended. Also, whenever the exact Hessian can be easily provided, IMSL routine UMIAH should be used instead.
Comments
1. Workspace may be explicitly provided, if desired, by use of U2IDH/DU2IDH. The reference is:
CALL U2IDH (FCN, GRAD, N, XGUESS, XSCALE, FSCALE, IPARAM, RPARAM, X, FVALUE, WK)
The additional argument is:
WK Work vector of length N * (N + 9). WK contains the following information on output: The second N locations contain the last step taken. The third N locations contain the last Newton step. The fourth N locations contain an estimate of the gradient at the solution. The final N2 locations contain the Hessian at the approximate solution.
2. Informational errors
Type Code
3 1 Both the actual and predicted relative reductions in the function are less than or equal to the relative function convergence tolerance.
4 2 The iterates appear to be converging to a noncritical point.
4 3 Maximum number of iterations exceeded.
4 4 Maximum number of function evaluations exceeded.
4 5 Maximum number of gradient evaluations exceeded.
4 6 Five consecutive steps have been taken with the maximum step length.
2 7 Scaled step tolerance satisfied; the current point may be an approximate local solution, or the algorithm is making very slow progress and is not near a solution, or STEPTL is too big.
4 7 Maximum number of Hessian evaluations exceeded.
3 8 The last global step failed to locate a lower point than the current X value.
3. The first stopping criterion for UMIDH occurs when the norm of the gradient is less than the given gradient tolerance (RPARAM(1)). The second stopping criterion for UMIDH occurs when the scaled distance between the last two steps is less than the step tolerance (RPARAM(2)).
4. If the default parameters are desired for UMIDH, then set IPARAM(1) to zero and call routine UMIDH. Otherwise, if any nondefault parameters are desired for IPARAM or RPARAM, then the following steps should be taken before calling UMIDH:
CALL U4INF (IPARAM, RPARAM)
Set nondefault values for desired IPARAM, RPARAM elements.
Note that the call to U4INF will set IPARAM and RPARAM to their default values so only nondefault values need to be set above.
The following is a list of the parameters and the default values:
IPARAM Integer vector of length 7.
IPARAM(1) = Initialization flag.
IPARAM(2) = Number of good digits in the function.
Default: Machine dependent.
IPARAM(3) = Maximum number of iterations.
Default: 100.
IPARAM(4) = Maximum number of function evaluations.
Default: 400.
IPARAM(5) = Maximum number of gradient evaluations.
Default: 400.
IPARAM(6) = Hessian initialization parameter
Default: Not used in UMIDH.
IPARAM(7) = Maximum number of Hessian evaluations.
Default:100
RPARAM Real vector of length
7.
RPARAM(1) = Scaled gradient
tolerance.
The i-th component of the scaled gradient at x is
calculated as
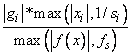
where g = ∇f (x), s = XSCALE, and fs = FSCALE.
Default:
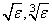
in double where ɛ is the machine precision.
RPARAM(2) = Scaled step tolerance. (STEPTL)
The i-th component of the scaled step between two points x and y is computed as
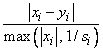
where s = XSCALE.
Default: ɛ2/3 where ɛ is the machine precision.
RPARAM(3) = Relative function tolerance.
Default: max(10-10, ɛ2/3), max(10-20, ɛ2/3) in double where ɛ is the machine precision.
RPARAM(4) = Absolute function tolerance.
Default: Not used in UMIDH.
RPARAM(5) = False convergence tolerance.
Default: 100ɛ where ɛ is the machine precision.
RPARAM(6) = Maximum allowable step size.
Default: 1000 max(ɛ1, ɛ2) where
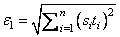
ɛ2 = || s ||2, s = XSCALE, and t = XGUESS.
RPARAM(7) = Size of initial trust region radius.
Default: Based on initial scaled Cauchy step.
If double precision is required, then DU4INF is called, and RPARAM is declared double precision.
5. Users wishing to override the default print/stop attributes associated with error messages issued by this routine are referred to Error Handling in the Introduction.
Example
The function
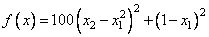
is minimized. Default values for parameters are used.
USE UMIDH_INT
USE UMACH_INT
IMPLICIT NONE
INTEGER N
PARAMETER (N=2)
!
INTEGER IPARAM(7), L, NOUT
REAL F, X(N), XGUESS(N)
EXTERNAL ROSBRK, ROSGRD
!
DATA XGUESS/-1.2E0, 1.0E0/
!
IPARAM(1) = 0
! Minimize Rosenbrock function using
! initial guesses of -1.2 and 1.0
CALL UMIDH (ROSBRK, ROSGRD, X, XGUESS=XGUESS, IPARAM=IPARAM, FVALUE=F)
! Print results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) X, F, (IPARAM(L),L=3,5), IPARAM(7)
!
99999 FORMAT (' The solution is ', 6X, 2F8.3, //, ' The function ', &
'value is ', F8.3, //, ' The number of iterations is ', &
10X, I3, /, ' The number of function evaluations is ', &
I3, /, ' The number of gradient evaluations is ', I3, /, &
' The number of Hessian evaluations is ', I3)
!
END
!
SUBROUTINE ROSBRK (N, X, F)
INTEGER N
REAL X(N), F
!
F = 1.0E2*(X(2)-X(1)*X(1))**2 + (1.0E0-X(1))**2
!
RETURN
END
!
SUBROUTINE ROSGRD (N, X, G)
INTEGER N
REAL X(N), G(N)
!
G(1) = -4.0E2*(X(2)-X(1)*X(1))*X(1) - 2.0E0*(1.0E0-X(1))
G(2) = 2.0E2*(X(2)-X(1)*X(1))
!
RETURN
END
Output
The solution
is 1.000
1.000
The function value is 0.000
The number of
iterations is
21
The number of function evaluations is 30
The number of gradient
evaluations is 22
The number of Hessian evaluations is
21
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |