Finds the minimum point of a nonsmooth function of a single variable.

Required Arguments

F — User-supplied function to compute the value of the function to be minimized. The form is F(X), where

X – The point at which the function is evaluated.   (Input)
X should not be changed by F.

F – The computed function value at the point X.   (Output)

F must be declared EXTERNAL in the calling program.

A — On input, A is the lower endpoint of the interval in which the minimum of F is to be located. On output, A is the lower endpoint of the interval in which the minimum of F is located.   (Input/Output)

B — On input, B is the upper endpoint of the interval in which the minimum of F is to be located. On output, B is the upper endpoint of the interval in which the minimum of F is located.   (Input/Output)

XMIN — The approximate minimum point of the function F on the original interval (A, B).   (Output)

Optional Arguments

TOL — The allowable length of the final subinterval containing the minimum point.   (Input)
Default: TOL = 1.e-4.

FORTRAN 90 Interface

Generic:          CALL UVMGS (F, A, B, XMIN [,…])

Specific:         The specific interface names are S_UVMGS and D_UVMGS.

FORTRAN 77 Interface

Single:            CALL UVMGS (F, A, B, TOL, XMIN)

Double:          The double precision name is DUVMGS.

Description

The routine UVMGS uses the golden section search technique to compute to the desired accuracy the independent variable value that minimizes a unimodal function of one independent variable, where a known finite interval contains the minimum.

Let τ = TOL. The number of iterations required to compute the minimizing value to accuracy τ is the greatest integer less than or equal to

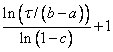
where a and b define the interval and

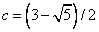
The first two test points are v1 and v2 that are defined as

v1 = a + c(b - a), and v2 = b - c(b - a)

If f(v1) < f(v2), then the minimizing value is in the interval (a, v2). In this case, b ← v2, v2 ← v1 , and v1 ← a + c(b - a). If f(v1) ≥ f(v2), the minimizing value is in (v1, b). In this case, a ← v1,
 v1 ← v2, and v2← b - c(b - a).

The algorithm continues in an analogous manner where only one new test point is computed at each step. This process continues until the desired accuracy τ is achieved. XMIN is set to the point producing the minimum value for the current iteration.

Mathematically, the algorithm always produces the minimizing value to the desired accuracy; however, numerical problems may be encountered. If f is too flat in part of the region of interest, the function may appear to be constant to the computer in that region. Error code 2 indicates that this problem has occurred. The user may rectify the problem by relaxing the requirement on τ, modifying (scaling, etc.) the form of f or executing the program in a higher precision.

Comments

1.         Informational errors

Type   Code

3                               TOL is too small to be satisfied.

4           2                  Due to rounding errors F does not appear to be unimodal.

2.         On exit from UVMGS without any error messages, the following conditions hold:
 (B-A) ≤ TOL.
A ≤ XMIN and XMIN ≤ B
F(XMIN) ≤ F(A) and F(XMIN) ≤ F(B)

3.         On exit from UVMGS with error code 2, the following conditions hold:
A ≤ XMIN and XMIN ≤ B
F(XMIN) ≥ F(A) and F(XMIN) ≥ F(B) (only one equality can hold).
Further analysis of the function F is necessary in order to determine whether it is not unimodal in the mathematical sense or whether it appears to be not unimodal to the routine due to rounding errors in which case the A, B, and XMIN returned may be acceptable.

Example

A minimum point of 3x2 - 2x + 4 is found.

 

      USE UVMGS_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                                 Specification of variables

      INTEGER    NOUT

      REAL       A, B, FCN, FMIN, TOL, XMIN

      EXTERNAL   FCN

!                                 Initialize variables

      A   = 0.0E0

      B   = 5.0E0

      TOL = 1.0E-3

!                                 Minimize FCN

      CALL UVMGS (FCN, A, B, XMIN, TOL=TOL)

      FMIN = FCN(XMIN)

!                                 Print results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) XMIN, FMIN, A, B

99999 FORMAT ('   The minimum is at ', F5.3, //, '   The ', &

            'function value is ', F5.3, //, '   The final ', &

            'interval is (', F6.4, ',', F6.4, ')', /)

!

      END

!

!                                 REAL FUNCTION: F = 3*X**2 - 2*X + 4

      REAL FUNCTION FCN (X)

      REAL       X

!

      FCN = 3.0E0*X*X - 2.0E0*X + 4.0E0

!

      RETURN

      END

Output

 

The minimum is at 0.333

The function value is 3.667

The final interval is (0.3331,0.3340)

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260