This function evaluates the chi-squared cumulative distribution function.
Function Return Value
CHIDF — Function value, the probability that a chi-squared random variable takes a value less than or equal to CHSQ. (Output)
Required Arguments
CHSQ — Argument for which the chi-squared distribution function is to be evaluated. (Input)
DF — Number of
degrees of freedom of the chi-squared distribution. (Input)
DF must be
greater than or equal to 0.5.
FORTRAN 90 Interface
Generic: CHIDF (CHSQ, DF)
Specific: The specific interface names are S_CHIDF and D_CHIDF.
FORTRAN 77 Interface
Single: CHIDF (CHSQ, DF)
Double: The double precision name is DCHIDF.
Description
Function CHIDF evaluates the cumulative distribution function, F, of a chi-squared random variable with DF degrees of freedom, that is, with v = DF, and x = CHSQ,
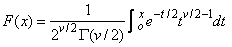
where G(×) is the gamma function. The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.
For v > 65, CHIDF uses the Wilson-Hilferty approximation (Abramowitz and Stegun 1964, equation 26.4.17) to the normal distribution, and routine ANORDF is used to evaluate the normal distribution function.
For v ≤ 65, CHIDF uses series expansions to evaluate the distribution function. If x < max (v/2, 26), CHIDF uses the series 6.5.29 in Abramowitz and Stegun (1964), otherwise, it uses the asymptotic expansion 6.5.32 in Abramowitz and Stegun.

Figure 11- 8 Chi-Squared Distribution Function
Comments
Informational errors
Type Code
1 1 Since the input argument, CHSQ, is less than zero, the distribution function is zero at CHSQ.
2 3 The normal distribution is used for large degrees of freedom. However, it has produced underflow. Therefore, the probability, CHIDF, is set to zero.
Example
Suppose X is a chi-squared random variable with 2 degrees of freedom. In this example, we find the probability that X is less than 0.15 and the probability that X is greater than 3.0.
USE UMACH_INT
USE CHIDF_INT
IMPLICIT NONE
INTEGER NOUT
REAL CHSQ, DF, P
!
CALL UMACH (2, NOUT)
DF = 2.0
CHSQ = 0.15
P = CHIDF(CHSQ,DF)
WRITE (NOUT,99998) P
99998 FORMAT (' The probability that chi-squared with 2 df is less ', &
'than 0.15 is ', F6.4)
CHSQ = 3.0
P = 1.0 - CHIDF(CHSQ,DF)
WRITE (NOUT,99999) P
99999 FORMAT (' The probability that chi-squared with 2 df is greater ' &
, 'than 3.0 is ', F6.4)
END
Output
The probability that chi-squared with 2 df is less than 0.15 is 0.0723
The probability that chi-squared with 2 df is greater than 3.0 is 0.2231
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |