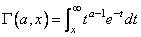Evaluates the complementary incomplete gamma function.

Function Return Value

GAMIC — Function value.   (Output)

Required Arguments

A — The integrand exponent parameter as per the remarks.   (Input)

X — The upper limit of the integral definition of GAMIC.   (Input)
If A is positive, then X must be positive. Otherwise, X must be nonnegative.

FORTRAN 90 Interface

Generic:                              GAMIC (A, X)

Specific:                             The specific interface names are S_GAMIC and D_GAMIC.

FORTRAN 77 Interface

Single:                                GAMIC (A, X)

Double:                              The double precision function name is DGAMIC.

Description

The incomplete gamma function is defined to be

The only general restrictions on a are that it must be positive if x is zero; otherwise, it must not be too close to a negative integer such that the accuracy of the result is less than half precision. Furthermore, G(a, x) must not be so small that it underflows, or so large that it overflows. Although G(a, x) is well defined for x >-∞ and a > 0, this algorithm does not calculate G(a, x) for negative x.

The function GAMIC is based on a code by Gautschi (1979).

Comments

Informational error

Type           Code

3                   2          Result of GAMIC(A, X) is accurate to less than one-half precision because A is too near a negative integer.

Example

In this example, G(2.5, 0.9) is computed and printed.

 

      USE GAMIC_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                                 Declare variables

      INTEGER    NOUT

      REAL       A, VALUE, X

!                                 Compute

      A     = 2.5

      X     = 0.9

      VALUE = GAMIC(A, X)

!                                 Print the results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) A, X, VALUE

99999 FORMAT (' GAMIC(', F6.3, ',', F6.3, ') = ', F6.4)

      END

Output

 

GAMIC( 2.500, 0.900) = 1.1646

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260