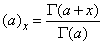This function evaluates a generalization of Pochhammer's symbol.
Function Return Value
POCH — Function
value. (Output)
The generalized Pochhammer symbol is G(a
+ x)/ G(a).
Required Arguments
A — The first argument. (Input)
X — The second, differential argument. (Input)
FORTRAN 90 Interface
Specific: The specific interface names are S_POCH and D_POCH.
FORTRAN 77 Interface
Double: The double precision function name is DPOCH.
Description
Pochhammer's symbol is (a)n = (a)(a - 1)¼(a - n + 1) for n a nonnegative integer. Pochhammer's generalized symbol is defined to be
See GAMMA for the definition of G(x).
Note that a straightforward evaluation of Pochhammer's generalized symbol with either gamma or log gamma functions can be especially unreliable when a is large or x is small.
Substantial loss can occur if a + x or a are close to a negative integer unless |x| is sufficiently small. To insure that the result does not overflow or underflow, one can keep the arguments a and a + x well within the range dictated by the gamma function routine GAMMA or one can keep |x| small whenever a is large. POCH also works for a variety of arguments outside these rough limits, but any more general limits that are also useful are difficult to specify.
Comments
3 2 Result of POCH(A, X) is accurate to less than one-half precision because the absolute value of the X is too large. Therefore, A + X cannot be evaluated accurately.
3 2 Result of POCH(A, X) is accurate to less than one-half precision because either A or A + X is too close to a negative integer.
For X a nonnegative integer, POCH(A, X) is just Pochhammer's symbol.
Example
In this example, (1.6)0.8 is computed and printed.
WRITE (NOUT,99999) A, X, VALUE
99999 FORMAT (' POCH(', F6.3, ',', F6.3, ') = ', F6.4)
Output
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |