The function evaluates the logarithm of the absolute value of the gamma function.
Function Return Value
ALNGAM — Function value. (Output)
Required Arguments
X — Argument for which the function value is desired. (Input)
FORTRAN 90 Interface
Generic: ALNGAM (X)
Specific: The specific interface names are S_ALNGAM, D_ALNGAM, and C_ALNGAM.
FORTRAN 77 Interface
Single: ALNGAM (X)
Double: The double precision function name is DLNGAM.
Complex: The complex name is CLNGAM.
Description
The function ALNGAM computes ln |Γ(x)|. See GAMMA for the definition of Γ(x).
The gamma function is not defined for integers less than or equal to zero. Also, |x| must not be so large that the result overflows. Neither should x be so close to a negative integer that the accuracy is worse than half precision.
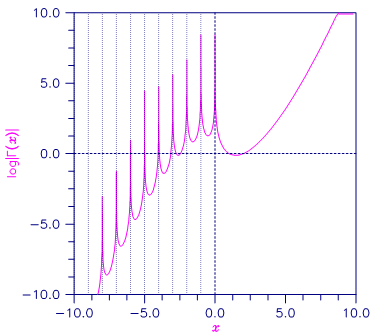
Figure 4- 2 Plot of log|Γ(x)|
Comments
Informational error
Type Code
3 2 Result of ALNGAM(X) is accurate to less than one-half precision because X is too near a negative integer.
Example 1
In this example, ln |Γ(1.85)| is computed and printed.
USE ALNGAM_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
REAL VALUE, X
! Compute
X = 1.85
VALUE = ALNGAM(X)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) X, VALUE
99999 FORMAT (' ALNGAM(', F6.3, ') = ', F6.3)
END
Output
ALNGAM( 1.850) = -0.056
Additional Example
Example 2
In this example, ln Γ(1.4 + 3i) is computed and printed.
USE ALNGAM_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
COMPLEX VALUE, Z
! Compute
Z = (1.4, 3.0)
VALUE = ALNGAM(Z)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) Z, VALUE
99999 FORMAT (' ALNGAM(', F6.3, ',', F6.3, ') = (',&
F6.3, ',', F6.3, ')')
END
Output
ALNGAM( 1.400, 3.000) = (-2.795, 1.589)
|
PHONE: 713.784.3131 FAX:713.781.9260 |