This function extends FORTRAN's generic function ATAN2 to evaluate the complex arc tangent of a ratio.

Function Return Value

ATAN2 — Complex function value in units of radians with the real part between -π and π.   (Output)

Required Arguments

CSN — Complex numerator of the ratio for which the arc tangent is desired.   (Input)

CCS — Complex denominator of the ratio.   (Input)

FORTRAN 90 Interface

Generic:                              ATAN2 (CSN, CCS)

Specific:                             The specific interface names are CATAN2 and ZATAN2.

FORTRAN 77 Interface

Complex:                            CATAN2 (CSN, CCS)

Double complex:               The double complex function name is ZATAN2.

Description

Let z₁ = CSN and z₂ = CCS. The ratio z = z₁/z₂ must not be ± i because tan^-1 (± i) is undefined. Likewise, z₁  and z₂ should not both be zero. Finally, z must not be so close to ±i that substantial accuracy loss occurs.

Comments

The result is returned in the correct quadrant (modulo 2 π).

Example

In this example,

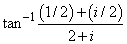
is computed and printed.

 

      USE ATAN2_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                                 Declare variables

      INTEGER    NOUT

      COMPLEX    VALUE, X, Y

!                                 Compute

      X     = (2.0, 1.0)

      Y     = (0.5, 0.5)

      VALUE = ATAN2(Y, X)

!                                 Print the results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) Y, X, VALUE

99999 FORMAT (' ATAN2((', F6.3, ',', F6.3, '), (', F6.3, ',', F6.3,&

          ')) = (', F6.3, ',', F6.3, ')')

      END

Output

 

ATAN2(( 0.500, 0.500), ( 2.000, 1.000)) = ( 0.294, 0.092)

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260