This function evaluates the exponentially scaled derivative of the Airy function of the second kind.
Function Return Value
BIDE — Function
value. (Output)
The derivative of the Airy function of the
second kind for negative arguments and the exponentially scaled derivative of
the Airy function of the second kind, eζBiʹ(X), for positive
arguments where
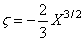
Required Arguments
X — Argument for which the Airy function value is desired. (Input)
FORTRAN 90 Interface
Generic: BIDE (X)
Specific: The specific interface names are S_BIDE and D_BIDE.
FORTRAN 77 Interface
Single: BIDE (X)
Double: The double precision name is DBIDE.
Description
The exponentially scaled derivative of the Airy function of the second kind is defined to be
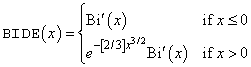
If 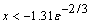 , then the answer will have
no precision. If
, then the answer will have
no precision. If 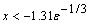 , then the answer will be
less accurate than half precision. Here, ε = AMACH(4)
is the machine precision.
, then the answer will be
less accurate than half precision. Here, ε = AMACH(4)
is the machine precision.
Example
In this example, BIDE(0.49) is computed and printed.
USE BIDE_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
REAL VALUE, X
! Compute
X = 0.49
VALUE = BIDE(X)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) X, VALUE
99999 FORMAT (' BIDE(', F6.3, ') = ', F6.3)
END
Output
BIDE( 0.490) = 0.430
|
PHONE: 713.784.3131 FAX:713.781.9260 |