This function evaluates the binomial probability density function.

Function Return Value

BINPR   Function value, the probability that a binomial random variable takes a value equal to K.   (Output)

Required Arguments

K — Argument for which the binomial probability function is to be evaluated.   (Input)

N — Number of Bernoulli trials.   (Input)

PIN — Probability of success on each independent trial.   (Input)

FORTRAN 90 Interface

Generic:                              BINPR (K, N, PIN)

Specific:                             The specific interface names are S_BINPR and D_BINPR.

FORTRAN 77 Interface

Single:                                BINPR (K, N, PIN)

Double:                              The double precision name is DBINPR.

Description

The function BINPR evaluates the probability that a binomial random variable with parameters n and p where p =PIN takes on the value k. It does this by computing probabilities of the random variable taking on the values in its range less than (or the values greater than) k. These probabilities are computed by the recursive relationship

 

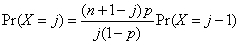
To avoid the possibility of underflow, the probabilities are computed forward from 0, if k is not greater than n times p, and are computed backward from n, otherwise. The smallest positive machine number, ε, is used as the starting value for computing the probabilities, which are rescaled by (1 − p)nε if forward computation is performed and by pnε if backward computation is done.

For the special case of p = 0, BINPR is set to 0 if k is greater than 0 and to 1 otherwise; and for the case p = 1, BINPR is set to 0 if k is less than n and to 1 otherwise.

Figure 11- 4  Binomial Probability Function

Comments

Informational errors

Type Code

1         3                  The input argument, K, is less than zero.

1         4                  The input argument, K, is greater than the number of Bernoulli trials, N.

Example

Suppose X is a binomial random variable with N = 5 and PIN = 0.95. In this example, we find the probability that X is equal to 3.

 

      USE UMACH_INT

      USE BINPR_INT

      IMPLICIT   NONE

      INTEGER    K, N, NOUT

      REAL       PIN, PR

!

      CALL UMACH (2, NOUT)

      K  = 3

      N  = 5

      PIN  = 0.95

      PR = BINPR(K,N,PIN)

      WRITE (NOUT,99999) PR

99999 FORMAT (' The probability that X is equal to 3 is ', F6.4)

      END

Output

 

The probability that X is equal to 3 is 0.0214

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260