This function evaluates the Bessel function of the first kind of order one.

Function Return Value

BSJ1 — Function value.   (Output)

Required Arguments

X — Argument for which the function value is desired.   (Input)

FORTRAN 90 Interface

Generic:                              BSJ1 (X)

Specific:                             The specific interface names are S_BSJ1 and D_BSJ1.

FORTRAN 77 Interface

Single:                                BSJ1 (X)

Double:                              The double precision function name is DBSJ1.

Description

The Bessel function J1(x) is defined to be

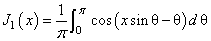
The argument x must be zero or larger in absolute value than 2s to prevent J1(x) from underflowing. Also, |x| should be smaller than

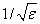
to prevent the answer from being less accurate than half precision. |x| must be less than 1/ε for the result to have any precision at all. Here, ε is the machine precision, ε = AMACH(4), and s = AMACH(1) is the smallest representable positive floating-point number.

Comments

Informational errors

Type Code

2         1                  The function underflows because the absolute value of X is too small.

Example

In this example, J1(2.5) is computed and printed.

 

      USE BSJ1_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                                 Declare variables

      INTEGER    NOUT

      REAL       VALUE, X

!                                 Compute

      X     = 2.5

      VALUE = BSJ1(X)

!                                 Print the results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) X, VALUE

99999 FORMAT (' BSJ1(', F6.3, ') = ', F6.3)

      END

Output

 

BSJ1( 2.500) =  0.497

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260